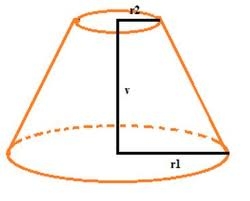
Truncated cone
Find the volume and surface area of the truncated cone if r1 = 12 cm, r2 = 5 cm, and side s = 10 cm.
Final Answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebrasolid geometryplanimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- The surface
The surface of a truncated rotating cone with side s = 13 cm is S = 510π cm². Find the radii of the bases when their difference in lengths is 10cm. - Frustrum - volume, area
Calculate the surface and volume of the truncated cone. The radius of the smaller figure is 4 cm, the height of the cone is 4 cm, and the side of the truncated cone is 5 cm. - Truncated cone
A truncated cone has bases with 40 cm and 10 cm radiuses and a height of 25 cm. Calculate its surface area and volume. - Frustrum - volume, area
Calculate the surface and volume of a truncated rotating cone with base radii of 8 cm and 4 cm and a height of 5 cm. - Truncated cone
Calculate the volume of a truncated cone with base radiuses r1=19 cm, r2 = 11 cm, and height v = 5 cm. - The cone - S,V
Calculate the volume and surface area of the cone if its radius r = 6 cm and side s = 10 cm. - Truncated pyramid
Find the volume and surface area of a regular quadrilateral truncated pyramid if base lengths a1 = 17 cm, a2 = 5 cm, and height v = 8 cm.
