Field with vegetables
The field planted with vegetables has a rectangular isosceles triangle with a leg length of 24 m. At the triangle's vertices are rotating sprinklers with a range of 12 m. How much of the field sprinkler doesn't irrigated?
Correct answer:

Tips for related online calculators
See also our right triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Cone
 The circular cone of height 15 cm and volume 5699 cm³ is at one-third of the height (measured from the bottom) cut by a plane parallel to the base. Calculate the radius and circumference of the circular cut.
The circular cone of height 15 cm and volume 5699 cm³ is at one-third of the height (measured from the bottom) cut by a plane parallel to the base. Calculate the radius and circumference of the circular cut. - Diagonals at right angle
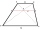 In the trapezoid ABCD, this is given: AB=12cm CD=4cm And diagonals crossed under a right angle. What is the area of this trapezoid ABCD?
In the trapezoid ABCD, this is given: AB=12cm CD=4cm And diagonals crossed under a right angle. What is the area of this trapezoid ABCD? - Ice cream
 Annie likes ice cream. In the shop are six kinds of ice cream. How many ways can she buy ice cream in three scoops if each has a different flavor mound and the order of scoops doesn't matter?
Annie likes ice cream. In the shop are six kinds of ice cream. How many ways can she buy ice cream in three scoops if each has a different flavor mound and the order of scoops doesn't matter? - Doesn't 37531
 How many ways can you draw eight playing cards from 32 playing cards when their order doesn't matter?
How many ways can you draw eight playing cards from 32 playing cards when their order doesn't matter?
- Medicine
 We test medicine on six patients. For all, the drug doesn't work. If the drug success rate of 20%, what is the probability that medicine does not work?
We test medicine on six patients. For all, the drug doesn't work. If the drug success rate of 20%, what is the probability that medicine does not work? - Classmate 2613
 Juro didn't have a watch, so he asked a classmate for the exact time. Simon looked at the clock and said: "If my watch were 22 minutes late, it would be 11:54. But it's not that much because my watch doesn't miss; it goes 22 minutes ahead". What time was
Juro didn't have a watch, so he asked a classmate for the exact time. Simon looked at the clock and said: "If my watch were 22 minutes late, it would be 11:54. But it's not that much because my watch doesn't miss; it goes 22 minutes ahead". What time was - Hypotenuse 79904
 I have a right triangle, the length of the hypotenuse is c 20, and I only know the side ratio a:b = 2:1. I can't figure out the actual length of the hangers = I'm already an old man, and my brain doesn't work at 100% like it did years ago at school - I co
I have a right triangle, the length of the hypotenuse is c 20, and I only know the side ratio a:b = 2:1. I can't figure out the actual length of the hangers = I'm already an old man, and my brain doesn't work at 100% like it did years ago at school - I co - Water 63
 Boiler heated water at the rate of 6°c per minute for 14 minutes. It then cooled at the rate of 8°c per minute. What would be its temperature after 24 minutes if its original temperature was 40°c?
Boiler heated water at the rate of 6°c per minute for 14 minutes. It then cooled at the rate of 8°c per minute. What would be its temperature after 24 minutes if its original temperature was 40°c? - Tarzan
 Tarzan, weighing m = 90 kg, tries to cross the river by swinging with a vine hanging from a tree leaning over the river. Liana has a length l = 12 m. The speed of the Tarzan in the lowest swing position is v = 8 m/s. Tarzan doesn't know that the liana wil
Tarzan, weighing m = 90 kg, tries to cross the river by swinging with a vine hanging from a tree leaning over the river. Liana has a length l = 12 m. The speed of the Tarzan in the lowest swing position is v = 8 m/s. Tarzan doesn't know that the liana wil
- Isosceles 67744
 Two isosceles triangles have the same angle at the vertex opposite the base. The first one has a base of 12 cm and a leg of 9 cm. The other has a 16 cm long base. Calculate the perimeter of the second triangle.
Two isosceles triangles have the same angle at the vertex opposite the base. The first one has a base of 12 cm and a leg of 9 cm. The other has a 16 cm long base. Calculate the perimeter of the second triangle. - Ladislav in Amsterdam
 Laco went (was sent) to a conference in Amsterdam for a reward. The conference fee was € 1304. Calculate how many books Ladislav could buy at the price of 32 and 22 euros if he doesn't want to fill the whole home library, and he can buy only 52 books
Laco went (was sent) to a conference in Amsterdam for a reward. The conference fee was € 1304. Calculate how many books Ladislav could buy at the price of 32 and 22 euros if he doesn't want to fill the whole home library, and he can buy only 52 books - Thinking 4586
 I'm thinking of a number that doesn't belong to the group. Please find it, justify the choice, and divide it by 9. 36,54,56,80,72,64,42,18,24,32,90,48,28,99.
I'm thinking of a number that doesn't belong to the group. Please find it, justify the choice, and divide it by 9. 36,54,56,80,72,64,42,18,24,32,90,48,28,99. - Isosceles 48443
 Three equal positive charges Q are located at the vertices of an isosceles right triangle ABC. The right angle is at vertex A. The length of side AB is 1m. What is the electric field strength at the center S of side BC, i.e., what force would act on a pos
Three equal positive charges Q are located at the vertices of an isosceles right triangle ABC. The right angle is at vertex A. The length of side AB is 1m. What is the electric field strength at the center S of side BC, i.e., what force would act on a pos - Wednesday 3171
 What doesn't apply to him if the month is 31 days and five Mondays? A-5 Saturday B-5 Sunday C-5 Tuesdays D-5 Wednesday E-5 Thursdays?
What doesn't apply to him if the month is 31 days and five Mondays? A-5 Saturday B-5 Sunday C-5 Tuesdays D-5 Wednesday E-5 Thursdays?
- Six attractions
 How many opportunities do you have if you want to complete ten rides on the fair, but there are only six attractions?
How many opportunities do you have if you want to complete ten rides on the fair, but there are only six attractions? - Glass of juice
 The glass of juice-shaped cylinder 16 cm height and base diameter of 9 cm is filled with juice so that the level is 1 cm below the rim of the glass. Determine the maximum angle of the cup that we can tilt so the juice doesn't overflow.
The glass of juice-shaped cylinder 16 cm height and base diameter of 9 cm is filled with juice so that the level is 1 cm below the rim of the glass. Determine the maximum angle of the cup that we can tilt so the juice doesn't overflow. - Owl A,B,C
 Owl a gives a hoot every 7 minutes. Owl b gives a hoot every 9 minutes. Owl c gives a hoot every 5 minutes except when he has heard owl a or b give a hoot within the previous 2.5 minutes. If this happens, owl c doesn't give a hoot. If all three owls give
Owl a gives a hoot every 7 minutes. Owl b gives a hoot every 9 minutes. Owl c gives a hoot every 5 minutes except when he has heard owl a or b give a hoot within the previous 2.5 minutes. If this happens, owl c doesn't give a hoot. If all three owls give
