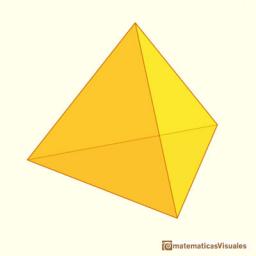
Triangular pyramid
Calculate the volume and surface area of a regular triangular pyramid with a height equal to the base edge, which is 10 cm long.
Final Answer:
Tips for related online calculators
See also our right triangle calculator.
Do you want to convert length units?
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
Do you want to convert length units?
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
arithmeticsolid geometryplanimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Quadrilateral pyramid
 Calculate the surface area and volume of a regular quadrilateral pyramid whose base edge is 5 cm long and whose height is 10 cm.
Calculate the surface area and volume of a regular quadrilateral pyramid whose base edge is 5 cm long and whose height is 10 cm. - Quadrilateral pyramid
 We have a regular quadrilateral pyramid with a base edge a = 10 cm and a height v = 7 cm. Calculate 1/base area 2/casing area 3/pyramid surface 4/volume of the pyramid
We have a regular quadrilateral pyramid with a base edge a = 10 cm and a height v = 7 cm. Calculate 1/base area 2/casing area 3/pyramid surface 4/volume of the pyramid - Triangular pyramid
 Determine the volume and surface area of a regular triangular pyramid having a base edge a=20 cm and a lateral edge b = 35 cm.
Determine the volume and surface area of a regular triangular pyramid having a base edge a=20 cm and a lateral edge b = 35 cm. - Regular triangular pyramid
 Calculate the volume and surface area of the regular triangular pyramid. The height of the pyramid is 12 centimeters. The bottom edge is 4 centimeters, and the height of the sidewall is 12 centimeters.
Calculate the volume and surface area of the regular triangular pyramid. The height of the pyramid is 12 centimeters. The bottom edge is 4 centimeters, and the height of the sidewall is 12 centimeters. - Calculate 4S pyramid
 Calculate the surface area and volume of a regular 4-sided pyramid with a base edge of a = 12 cm and a height of v = 5 cm.
Calculate the surface area and volume of a regular 4-sided pyramid with a base edge of a = 12 cm and a height of v = 5 cm. - Pyramid 4sides
 Calculate the volume and the surface of a regular quadrangular pyramid when the edge of the base is 4 cm long, and the pyramid's height is 7 cm.
Calculate the volume and the surface of a regular quadrangular pyramid when the edge of the base is 4 cm long, and the pyramid's height is 7 cm. - Triangular pyramid
 The regular triangular pyramid ABCDV has a base edge length of 8 cm and a height of 7 cm. Calculate the pyramid's surface area and volume.
The regular triangular pyramid ABCDV has a base edge length of 8 cm and a height of 7 cm. Calculate the pyramid's surface area and volume.
