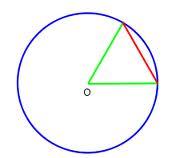
Chord
The point on the circle is the endpoint of diameter and endpoint of the chord length of the radius. What angle between chord and diameter?
Final Answer:
Tips for related online calculators
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
planimetricsUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Two chords
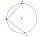There is a given circle k (center S, radius r). From point A, which lies on circle k, are starting two chords of length r. What angle do chords make? Draw and measure. - Two chords
From the point on the circle with a diameter of 8 cm, two identical chords are led, which form an angle of 60°. Calculate the length of these chords. - Circle and chord
The chord of a circle is 233 long, and the length of the circular arc above the chord is 235. What is the circle's radius, and what is the central angle of the circular arc? - Convex angle
There is a circle k (S; r), and a point A, which lies on this circle. There is also a point B on the circumference, for which it is true that in one direction, it is five times further from point A than in the opposite direction (around the circumference - Chord 2
Point A has a distance of 13 cm from the circle's center with a radius r = 5 cm. Calculate the length of the chord connecting the points T1 and T2 of contact of tangents led from point A to the circle. - Intersection + tangents
Given a circle with a radius r = 4 cm and a point A for which |AS| applies = 10 cm. Calculate the distance of point A from the intersection of the points of contact of the tangents drawn from point A to the circle. - Common chord
The common chord of the two circles, c1 and c2, is 3.8 cm long. This chord forms an angle of 47° with the radius r1 in the circle c1. An angle of 24° 30' with the radius r2 is formed in the circle c2. Calculate both radii and the distance between the two
