Billiard balls
A layer of ivory billiard balls radius of 6.35 cm is in the form of a square. The balls are arranged so that each ball is tangent to everyone adjacent to it. In the spaces between sets of 4 adjacent balls, other balls rest, equal in size to the original. These balls form, in turn, a second layer on top of the first. Successive layers of this sort form a pyramidal pile with a single ball resting on top. If the bottom layer contains 16 balls, what is the height of the pile?
Final Answer:

Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
algebrasolid geometryplanimetricsbasic operations and conceptsGrade of the word problem
Related math problems and questions:
- Tubes
 Iron tubes in the warehouse are stored in layers so that each tube's top layer fits into the gaps of the lower layer. How many layers are needed to deposit 100 tubes if the top layer has 9 tubes? How many tubes are in the bottom layer of tubes?
Iron tubes in the warehouse are stored in layers so that each tube's top layer fits into the gaps of the lower layer. How many layers are needed to deposit 100 tubes if the top layer has 9 tubes? How many tubes are in the bottom layer of tubes? - Sons
 The father has six sons and ten identical, indistinguishable balls. How many ways can he give the balls to his sons if everyone gets at least one?
The father has six sons and ten identical, indistinguishable balls. How many ways can he give the balls to his sons if everyone gets at least one? - Inscribed circle
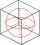 A circle is inscribed at the bottom wall of the cube with an edge (a = 1). What is the radius of the spherical surface that contains this circle and one of the vertex of the top cube base?
A circle is inscribed at the bottom wall of the cube with an edge (a = 1). What is the radius of the spherical surface that contains this circle and one of the vertex of the top cube base? - Book Store
 The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w
The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w - Diagonals 3580
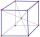 Cube edge length 5cm. Draw different diagonals.
Cube edge length 5cm. Draw different diagonals. - An experiment
 The three friends agreed to the experiment. At the same time, they all took out an empty cylindrical container on the windowsill and placed it so that it was horizontal. Everyone lives in a different village, and each uses a container with a different bot
The three friends agreed to the experiment. At the same time, they all took out an empty cylindrical container on the windowsill and placed it so that it was horizontal. Everyone lives in a different village, and each uses a container with a different bot - Gale and spruce
 A mighty gale broke the top of the fifteen-year spruce, resting it on the ground. The distance of this top from the trunk was 4.6 m below. At what height was the spruce trunk broken?
A mighty gale broke the top of the fifteen-year spruce, resting it on the ground. The distance of this top from the trunk was 4.6 m below. At what height was the spruce trunk broken?
