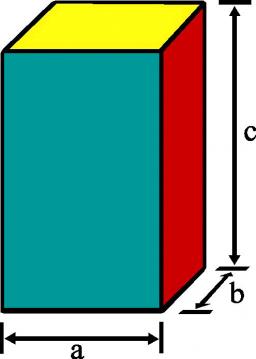
Cuboid and eq2

Calculate the volume of a cuboid with a square base and height of 6 cm if the surface area is 48 cm2.

Final Answer:

V =  18.2904 cm3

Step-by-step explanation:

h=6 cm S=48 cm2 S = 4ah +2a2 48=4⋅ 6⋅ a+2⋅ a2  48=4⋅ 6⋅ a+2⋅ a2 −2a2−24a+48=0 2a2+24a−48=0 2 ...  prime number 24=23⋅3 48=24⋅3 GCD(2,24,48)=2  a2+12a−24=0  p=1;q=12;r=−24 D=q2−4pr=122−4⋅1⋅(−24)=240 D>0  a1,2​=2p−q±D​​=2−12±240​​=2−12±415​​ a1,2​=−6±7.745967 a1​=1.745966692 a2​=−13.745966692  a=a1​=1.746≐1.746  V=a2⋅ h=1.7462⋅ 6≐18.2904 cm3   Verifying Solution:  S2​=4⋅ a⋅ h+2⋅ a2=4⋅ 1.746⋅ 6+2⋅ 1.7462=48 cm2 S2​=S

Our quadratic equation calculator calculates it.


Try another example


Did you find an error or inaccuracy? Feel free to write us. Thank you!







Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Tip: Our volume units converter will help you convert volume units.

You need to know the following knowledge to solve this word math problem:

algebrasolid geometryplanimetricsUnits of physical quantitiesGrade of the word problem

 
We encourage you to watch this tutorial video on this math problem: video1

Related math problems and questions: