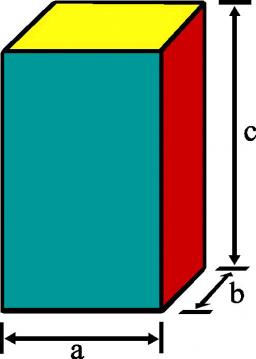
Cuboid and eq2
Calculate the volume of a cuboid with a square base and a height of 6 cm if its total surface area is 48 cm².
Your answer:
Your answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
Tip: Our volume units converter will help you convert volume units.
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
algebrasolid geometryplanimetryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Prism
Calculate the height of a prism with a total surface area of 448.88 dm² and a square base with a side of 6.2 dm. What is its volume in hectolitres? - Quadrilateral prism
Calculate the surface and volume of a quadrilateral prism if given: the area of the base is 40 cm², the bottom of the base is k = 8 cm, and the height of the prism is 1.3 dm (the bottom is a rectangle) - Cuboid Height from Surface
The cuboid with a base measuring 17 cm and 13 cm has a surface of 1342 cm². Calculate the height of the cuboid and sketch its network. - Regular square prism
The volume of a regular square prism is 192 cm³. The size of its base edge and the body height is 1:3. Calculate the surface of the prism. - Cuboid - sum of edges length
Calculate the cuboid's dimensions if the sum of its edges is 19 cm. The body's diagonal size is 13 cm, and its volume is 144 cm³. The total surface area is 192 cm². - The volume
The volume of a solid cylinder is 260 cm³. The cylinder is melted down into a cuboid whose base is a square of 5cm. Calculate the cuboid's height and surface area. - Cuboid surface calculation
We have a block with a square base and a height of 12 dm. We know that its volume is 588 cubic dm. Calculate the surface area of a cuboid with the same base but 2 cm more height. You write the result in dm².
