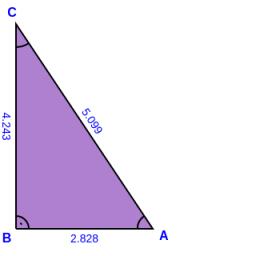
Right angled triangle 2
LMN is a right-angled triangle with vertices at L(1,3), M(3,5), and N(6,n). Given angle LMN is 90° find n
Final Answer:
Tips for related online calculators
The line slope calculator is helpful for basic calculations in analytic geometry. The coordinates of two points in the plane calculate slope, normal and parametric line equation(s), slope, directional angle, direction vector, the length of the segment, intersections of the coordinate axes, etc.
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
geometryalgebraplanimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Trapezoid - RR
 Find the area of the right-angled trapezoid ABCD with the right angle at the A vertex; a = 3 dm b = 5 dm c = 6 dm d = 4 dm
Find the area of the right-angled trapezoid ABCD with the right angle at the A vertex; a = 3 dm b = 5 dm c = 6 dm d = 4 dm - Know one angle
 In a right-angled triangle, the measure of an angle is 40°. Find the measure of other angles of the triangle in degrees.
In a right-angled triangle, the measure of an angle is 40°. Find the measure of other angles of the triangle in degrees. - Right-angled trapezoid
 A right-angled trapezoid with the measure of the acute angle of 50° is given. The lengths of its bases are 4 and 6 units. The volume of the solid obtained by rotation of the given trapezoid about the longer base is:
A right-angled trapezoid with the measure of the acute angle of 50° is given. The lengths of its bases are 4 and 6 units. The volume of the solid obtained by rotation of the given trapezoid about the longer base is: - A kite 3
 A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in th
A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in th - In a right-angled 17
 In a right-angled triangle DEF with hypotenuse f = 12 cm, the interior angle at vertex D is 60°. What is the length of the side e?
In a right-angled triangle DEF with hypotenuse f = 12 cm, the interior angle at vertex D is 60°. What is the length of the side e? - Triangle angle ratio
 In the right-angled triangle ABC (the right angle at vertex C), the angle ratio is α : β = 5 : 3. Calculate the sizes of these angles and convert them to degrees and minutes (e.g., 45°20')
In the right-angled triangle ABC (the right angle at vertex C), the angle ratio is α : β = 5 : 3. Calculate the sizes of these angles and convert them to degrees and minutes (e.g., 45°20') - Triangle's centroid
 In the triangle ABC the given lengths of its medians tc = 9, ta = 6. Let T be the intersection of the medians (triangle's centroid), and the point S is the center of the side BC. The magnitude of the CTS angle is 60°. Calculate the length of the BC side t
In the triangle ABC the given lengths of its medians tc = 9, ta = 6. Let T be the intersection of the medians (triangle's centroid), and the point S is the center of the side BC. The magnitude of the CTS angle is 60°. Calculate the length of the BC side t
