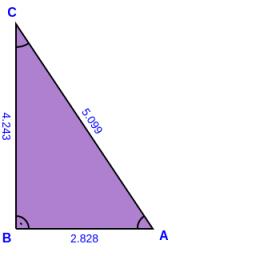
Right angled triangle 2

LMN is a right-angled triangle with vertices at L(1,3), M(3,5), and N(6,n). Given angle LMN is 90° find n

Final Answer:

n =  2

Step-by-step explanation:

n1​=(1−3)2+(3−5)2​=2 2​≐2.8284  m2 = (1−6)2 + (3−n)2  m2 = ((1−3)2+(3−5)2) + (3−6)2 + (5−n)2 (1−6)2 + (3−n)2 = (1−3)2+(3−5)2 + (3−6)2 + (5−n)2 4n = 8 n=8/4=2

Try calculation via our triangle calculator.


Try another example


Did you find an error or inaccuracy? Feel free to send us. Thank you!







Tips for related online calculators
The line slope calculator is helpful for basic calculations in analytic geometry. The coordinates of two points in the plane calculate slope, normal and parametric line equation(s), slope, directional angle, direction vector, the length of the segment, intersections of the coordinate axes, etc.
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.

You need to know the following knowledge to solve this word math problem:

geometryalgebraplanimetricsUnits of physical quantitiesGrade of the word problem

 
We encourage you to watch this tutorial video on this math problem: video1   video2

Related math problems and questions: