The Hotel
The Holiday Hotel has the same number of rooms on each floor. Rooms are numbered with natural numerals sequentially from the first floor, no number is omitted, and each room has a different number. Three tourists arrived at the hotel. The first one was in room number 50 on the fourth floor. The other room number is 100 on the seventh floor. Third is room number 126 on the ninth floor. How many rooms are on each floor?
Correct answer:

Tips for related online calculators
Do you solve Diofant problems and are looking for a calculator of Diofant integer equations?
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Remainder one
 Find the least number, when divided by 2,3,4,5,6 and 7 leaves remainder 1 in each case.
Find the least number, when divided by 2,3,4,5,6 and 7 leaves remainder 1 in each case. - 20 men
 20 men are supposed to complete a work in 10 days. After working for 5 days, they realize that only one-fourth of the work is done. How many more men they need to employ to complete the work on time?
20 men are supposed to complete a work in 10 days. After working for 5 days, they realize that only one-fourth of the work is done. How many more men they need to employ to complete the work on time? - Offset the mean
 The mean of 16 numbers is 8. If 2 is added to every number, what will be the new mean?
The mean of 16 numbers is 8. If 2 is added to every number, what will be the new mean? - Paul makes
 Paul makes a cuboid of plasticine of sides 5 cm, 2 cm, 5 cm. How many such cuboids will he need to form a cube?
Paul makes a cuboid of plasticine of sides 5 cm, 2 cm, 5 cm. How many such cuboids will he need to form a cube?
- Circumferences 83111
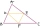 Péta composed several planar shapes from mutually congruent triangles. The circumferences of the first three are 8 cm, 11.4 cm, and 14.7 cm, respectively. Determine the perimeter of the fourth shape.
Péta composed several planar shapes from mutually congruent triangles. The circumferences of the first three are 8 cm, 11.4 cm, and 14.7 cm, respectively. Determine the perimeter of the fourth shape. - Gift baskets
 Alessia and Alexia made some gift baskets to sell. 2/5 of them were Yu-Gi-oh themed, and the rest were Barbie-themed. They sold 3/4 of the yu-gi-oh-themed baskets and 7/12 of the Barbie-themed baskets. They remained with 56 gift baskets. How many gift bas
Alessia and Alexia made some gift baskets to sell. 2/5 of them were Yu-Gi-oh themed, and the rest were Barbie-themed. They sold 3/4 of the yu-gi-oh-themed baskets and 7/12 of the Barbie-themed baskets. They remained with 56 gift baskets. How many gift bas - Five couples
 In how many ways can 5 couples arrange themselves in a row if they stay together?
In how many ways can 5 couples arrange themselves in a row if they stay together? - BODMAS rules
 To solve this problem using BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction), we need to arrange the numbers 50,5,1,10,1,10 in a way that results in 222.
To solve this problem using BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction), we need to arrange the numbers 50,5,1,10,1,10 in a way that results in 222. - Circle - analytics geometry
 Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0.
Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0.
- Arithmetic progressions.
 Find the sum of all the numbers between 9 and 204, which is exactly divisible by 3.
Find the sum of all the numbers between 9 and 204, which is exactly divisible by 3. - Hotel rooms 2
 Waterside bed and breakfast has 10 rooms. On average, they sell 8 rooms. The rate is $45 per night, bed and breakfast, $65 per night. Calculate the yield.
Waterside bed and breakfast has 10 rooms. On average, they sell 8 rooms. The rate is $45 per night, bed and breakfast, $65 per night. Calculate the yield. - Two-digit 82521
 Karel had to multiply two two-digit numbers. Out of care, he changed the order of the digits in one of the factors and got a product that was 4,248 less than the correct result. What is the correct result? How much should Karl have earned?
Karel had to multiply two two-digit numbers. Out of care, he changed the order of the digits in one of the factors and got a product that was 4,248 less than the correct result. What is the correct result? How much should Karl have earned? - Eggs in basket
 If the eggs in a basket are removed twice at a time, one will remain. Two eggs will remain if the eggs are removed three at a time. If the eggs are removed four, five, or six at a time, the three, four, and five eggs will remain, respectively. However, no
If the eggs in a basket are removed twice at a time, one will remain. Two eggs will remain if the eggs are removed three at a time. If the eggs are removed four, five, or six at a time, the three, four, and five eggs will remain, respectively. However, no - Department 82388
 Last year, there were 30 more boys than girls in our scout troop. This year, the number of children in the ward increased by 10%, while the number of boys increased by 5% and the number of girls increased by 20%. How many children do we have in the depart
Last year, there were 30 more boys than girls in our scout troop. This year, the number of children in the ward increased by 10%, while the number of boys increased by 5% and the number of girls increased by 20%. How many children do we have in the depart
- Three 241
 Three-fifths of the t-shirts in a t-shirt shop are blue. Five-eights of those T-shirts are on sale. One-third of the blue of the blue shirts that are on sale are size medium. What fraction of the shop's blue T-shirts are on sale and size medium?
Three-fifths of the t-shirts in a t-shirt shop are blue. Five-eights of those T-shirts are on sale. One-third of the blue of the blue shirts that are on sale are size medium. What fraction of the shop's blue T-shirts are on sale and size medium? - A ferry
 A ferry with a capacity of 10 people takes a group of 13 men and 7 women across a river. Find the number of ways in which the group may be taken across the if all women go on the first group.
A ferry with a capacity of 10 people takes a group of 13 men and 7 women across a river. Find the number of ways in which the group may be taken across the if all women go on the first group. - Five-digit 82257
 Determine the number of all five-digit natural numbers in which every two digits are different in decimal notation.
Determine the number of all five-digit natural numbers in which every two digits are different in decimal notation.
