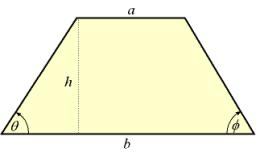
Isosceles trapezoid
Isosceles trapezoid ABCD, AB||CD is given by |CD| = c = 12 cm, height v = 16 cm and |CAB| = 20°. Calculate area of the trapezoid.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Isosceles 37621
 In the isosceles trapezoid ABCD, its bases AB = 20cm, CD = 12cm and arms AD = BC = 8cm are given. Specify its height and alpha angle at vertex A
In the isosceles trapezoid ABCD, its bases AB = 20cm, CD = 12cm and arms AD = BC = 8cm are given. Specify its height and alpha angle at vertex A - Circumference 7052
 The trapezoid ABCD is given (AB || CD, AB perpendicular to AD). Calculate its circumference if | AB | = 20cm, | CD | = 15cm, | AD | = 12cm. Pythagorean theorem
The trapezoid ABCD is given (AB || CD, AB perpendicular to AD). Calculate its circumference if | AB | = 20cm, | CD | = 15cm, | AD | = 12cm. Pythagorean theorem - Trapezoid 70454
 Construct a trapezoid ABCD (AB // CD): | AB | = 7cm | BC | = 3.5cm | CD | = 4cm The magnitude of the angle ABC = 60°
Construct a trapezoid ABCD (AB // CD): | AB | = 7cm | BC | = 3.5cm | CD | = 4cm The magnitude of the angle ABC = 60° - Trapezoid 20873
 In the trapezoid ABCD (AB II CD) is α = 57 °, γ = 4β. Calculate the size of all interior angles.
In the trapezoid ABCD (AB II CD) is α = 57 °, γ = 4β. Calculate the size of all interior angles.
- Isosceles 2588
 Given an isosceles trapezoid ABCD, in which | AB | = 2 | BC | = 2 | CD | = 2 | DA | holds. On its side BC, the point K is such that | BK | = 2 | KC |; on its CD side, the point L is such that | CL | = 2 | LD |, and on its DA side, the point M is such that
Given an isosceles trapezoid ABCD, in which | AB | = 2 | BC | = 2 | CD | = 2 | DA | holds. On its side BC, the point K is such that | BK | = 2 | KC |; on its CD side, the point L is such that | CL | = 2 | LD |, and on its DA side, the point M is such that - Diagonals at right angle
 In the trapezoid ABCD, this is given: AB=12cm CD=4cm And diagonals crossed under a right angle. What is the area of this trapezoid ABCD?
In the trapezoid ABCD, this is given: AB=12cm CD=4cm And diagonals crossed under a right angle. What is the area of this trapezoid ABCD? - Diagonal intersect
 Isosceles trapezoid ABCD with length bases | AB | = 6 cm, CD | = 4 cm is divided into four triangles by the diagonals intersecting at point S. How much of the area of the trapezoid are ABS and CDS triangles?
Isosceles trapezoid ABCD with length bases | AB | = 6 cm, CD | = 4 cm is divided into four triangles by the diagonals intersecting at point S. How much of the area of the trapezoid are ABS and CDS triangles?
