Volume + Pythagorean theorem - practice problems - page 3 of 15
Number of problems found: 289
- Calculate 66254
 Calculate the volume and surface of a regular hexagonal prism with a height v = 2cm and a base edge a = 8cm.
Calculate the volume and surface of a regular hexagonal prism with a height v = 2cm and a base edge a = 8cm. - Circumference 66134
 The isosceles trapezoid ABCD has an area of 36 cm². One of its bases is two times longer than the other. Height is 4 cm. Calculate the circumference of the trapezoid.
The isosceles trapezoid ABCD has an area of 36 cm². One of its bases is two times longer than the other. Height is 4 cm. Calculate the circumference of the trapezoid. - Mr. Bradshaw
 Mr. Bradshaw is leaning a ladder against the side of his house to repair the roof. The top of the ladder reaches the roof, which is 5 meters high. The ladder's base is 1 meter away from the house, where Mr. Bradshaw's son is holding it steady. How long is
Mr. Bradshaw is leaning a ladder against the side of his house to repair the roof. The top of the ladder reaches the roof, which is 5 meters high. The ladder's base is 1 meter away from the house, where Mr. Bradshaw's son is holding it steady. How long is - Trapezoid 65644
 In an isosceles trapezoid, the base ratio a / c = 9/7, arm b = 10 cm, height v = 8 cm. Calculate the area of the trapezoid in cm².
In an isosceles trapezoid, the base ratio a / c = 9/7, arm b = 10 cm, height v = 8 cm. Calculate the area of the trapezoid in cm².
- Measuring 65374
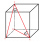 Calculate the length of the body diagonal of a block measuring 6 cm, 7 cm, and 10 cm, and round the result to two decimal places.
Calculate the length of the body diagonal of a block measuring 6 cm, 7 cm, and 10 cm, and round the result to two decimal places. - Calculate 65354
 Calculate the surface of a spherical paragraph with a height of 6 cm and a radius of 15 cm
Calculate the surface of a spherical paragraph with a height of 6 cm and a radius of 15 cm - Substantial 65114
 Calculate the volume of a regular triangular prism with a substantial edge length of 8 cm and a prism height of 17 cm.
Calculate the volume of a regular triangular prism with a substantial edge length of 8 cm and a prism height of 17 cm. - Calculate 65014
 The radius of the circle is 5.5 cm. The height is 2.3 cm, which is the chord's distance. How can we calculate the length of the string?
The radius of the circle is 5.5 cm. The height is 2.3 cm, which is the chord's distance. How can we calculate the length of the string? - Surface 64744
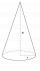 The cone is 12 cm high, and the radius of the figure is 9 cm. Find out its surface.
The cone is 12 cm high, and the radius of the figure is 9 cm. Find out its surface.
- Quadrangular 64724
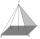 The decorative object has a quadrangular pyramid shape, the base edge is 0.7 dm, and the side edge is 1.4 dm long. Calculate the height of the object.
The decorative object has a quadrangular pyramid shape, the base edge is 0.7 dm, and the side edge is 1.4 dm long. Calculate the height of the object. - Magnitudes 64704
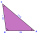 The triangle ABC determines the size of the sides a and b and the magnitudes of the interior angles β and γ, given c = 1.86 m, the line on the side c is 2.12 m, and the angle alpha is 40 ° 12 '.
The triangle ABC determines the size of the sides a and b and the magnitudes of the interior angles β and γ, given c = 1.86 m, the line on the side c is 2.12 m, and the angle alpha is 40 ° 12 '. - Calculate 64654
 Calculate the length of the wall and body diagonal in a cube with an edge of 60 cm.
Calculate the length of the wall and body diagonal in a cube with an edge of 60 cm. - Calculating 63344
 Calculate the volume of the cone formed by rotating an isosceles triangle about the height of the base. The triangle has a side length of 15 cm and a height to the base of 12 cm. When calculating, use the value pi = 3.14 and round the result to one decima
Calculate the volume of the cone formed by rotating an isosceles triangle about the height of the base. The triangle has a side length of 15 cm and a height to the base of 12 cm. When calculating, use the value pi = 3.14 and round the result to one decima - Prism - right isosceles
 Find the volume and surface of a prism with a height of 120 mm, the base of which is a right isosceles triangle with a leg length of 5 cm.
Find the volume and surface of a prism with a height of 120 mm, the base of which is a right isosceles triangle with a leg length of 5 cm.
- Side wall planes
 Find the volume and surface of a cuboid whose side c is 30 cm long and the body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls.
Find the volume and surface of a cuboid whose side c is 30 cm long and the body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls. - A prism
 A prism with an altitude of 15cm has a base in the form of a regular octagon inscribed in a square of 10cmx10cm. Find the volume of the prism.
A prism with an altitude of 15cm has a base in the form of a regular octagon inscribed in a square of 10cmx10cm. Find the volume of the prism. - Slant height 2
 A regular triangular pyramid with a slant height of 9 m has a volume of 50 m³. Find the lateral area of the pyramid.
A regular triangular pyramid with a slant height of 9 m has a volume of 50 m³. Find the lateral area of the pyramid. - A cone
 A cone measures 6 inches in diameter at the base. The distance from the edge of the circumference to the top is 12 inches. Find its volume.
A cone measures 6 inches in diameter at the base. The distance from the edge of the circumference to the top is 12 inches. Find its volume. - An equilateral cone
 Determine the radius and height (in centimeters) of an equilateral cone that has a volume of 1 liter.
Determine the radius and height (in centimeters) of an equilateral cone that has a volume of 1 liter.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
