Pythagorean theorem + volume - practice problems
Number of problems found: 289
- Calculate 415
 Calculate the cuboid's dimensions if the sum of its edges is 19cm. The body's diagonal size is 13 cm, and its volume is 144 cm³. The total surface area is 192 cm².
Calculate the cuboid's dimensions if the sum of its edges is 19cm. The body's diagonal size is 13 cm, and its volume is 144 cm³. The total surface area is 192 cm². - A frustum
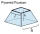 A frustum of a pyramid consists of a square base of length 10 cm and a top square of length 7 cm. The height of the frustum is 6 cm. Calculate the surface area and volume.
A frustum of a pyramid consists of a square base of length 10 cm and a top square of length 7 cm. The height of the frustum is 6 cm. Calculate the surface area and volume. - Calculate 2577
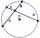 Calculate the length of the circle chord, which is 2.5 cm from the circle's center. The radius is 6.5 cm.
Calculate the length of the circle chord, which is 2.5 cm from the circle's center. The radius is 6.5 cm. - Calculate 65014
 The radius of the circle is 5.5 cm. The height is 2.3 cm, which is the chord's distance. How can we calculate the length of the string?
The radius of the circle is 5.5 cm. The height is 2.3 cm, which is the chord's distance. How can we calculate the length of the string?
- Perpendiculars 66274
 The perpendiculars of a right triangle have lengths of 30 cm and 40 cm. What is the height of the triangle?
The perpendiculars of a right triangle have lengths of 30 cm and 40 cm. What is the height of the triangle? - Rectangle 35
 Find the rectangle area when the diagonal is equal to 30 cm and the width is double the length.
Find the rectangle area when the diagonal is equal to 30 cm and the width is double the length. - Road embankment
 Road embankment has a cross-section shape of an isosceles trapezoid with bases 5 m and 7 m and 2 m long leg. How many cubic meters of soil is in embankment length of 1474 meters?
Road embankment has a cross-section shape of an isosceles trapezoid with bases 5 m and 7 m and 2 m long leg. How many cubic meters of soil is in embankment length of 1474 meters? - Silver medal
 A circular silver medal with a diameter of 10 cm is an inscribed gold cross consisting of five equal squares. What is the area of the silver part? b) What is the area of the golden cross?
A circular silver medal with a diameter of 10 cm is an inscribed gold cross consisting of five equal squares. What is the area of the silver part? b) What is the area of the golden cross? - Right-angled 82416
 What are the sides of a right-angled triangle with a perimeter of 45 centimeters and a volume of 67.5 cm²?
What are the sides of a right-angled triangle with a perimeter of 45 centimeters and a volume of 67.5 cm²?
- Trapezoid 65644
 In an isosceles trapezoid, the base ratio a / c = 9/7, arm b = 10 cm, height v = 8 cm. Calculate the area of the trapezoid in cm².
In an isosceles trapezoid, the base ratio a / c = 9/7, arm b = 10 cm, height v = 8 cm. Calculate the area of the trapezoid in cm². - Right-angled 66344
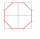 From a square with a side of 4 cm, we cut four right-angled isosceles triangles with right angles at the square's vertices and with an overlap of √2 cm. We get an octagon. Calculate its perimeter if the area of the octagon is 14 cm².
From a square with a side of 4 cm, we cut four right-angled isosceles triangles with right angles at the square's vertices and with an overlap of √2 cm. We get an octagon. Calculate its perimeter if the area of the octagon is 14 cm². - Cross-section 17871
 The road embankment has a cross-section of an isosceles trapezoid with bases 16 m and 10 m long and with arms 5 m long. How many cubic meters of soil is in the 400 m long dam?
The road embankment has a cross-section of an isosceles trapezoid with bases 16 m and 10 m long and with arms 5 m long. How many cubic meters of soil is in the 400 m long dam? - Circumference 66134
 The isosceles trapezoid ABCD has an area of 36 cm². One of its bases is two times longer than the other. Height is 4 cm. Calculate the circumference of the trapezoid.
The isosceles trapezoid ABCD has an area of 36 cm². One of its bases is two times longer than the other. Height is 4 cm. Calculate the circumference of the trapezoid. - Mr. Bradshaw
 Mr. Bradshaw is leaning a ladder against the side of his house to repair the roof. The top of the ladder reaches the roof, which is 5 meters high. The ladder's base is 1 meter away from the house, where Mr. Bradshaw's son is holding it steady. How long is
Mr. Bradshaw is leaning a ladder against the side of his house to repair the roof. The top of the ladder reaches the roof, which is 5 meters high. The ladder's base is 1 meter away from the house, where Mr. Bradshaw's son is holding it steady. How long is
- Magnitudes 64704
 The triangle ABC determines the size of the sides a and b and the magnitudes of the interior angles β and γ, given c = 1.86 m, the line on the side c is 2.12 m, and the angle alpha is 40 ° 12 '.
The triangle ABC determines the size of the sides a and b and the magnitudes of the interior angles β and γ, given c = 1.86 m, the line on the side c is 2.12 m, and the angle alpha is 40 ° 12 '. - Central park in city
 The city park has the shape of a rectangle of 180 meters in length and 120 meters in width. People make their walk through the center of the park from one corner to the second. Calculate how many meters this way is shorter than walking along the path arou
The city park has the shape of a rectangle of 180 meters in length and 120 meters in width. People make their walk through the center of the park from one corner to the second. Calculate how many meters this way is shorter than walking along the path arou - Chocolate roll
 The cube of 5 cm chocolate roll weighs 30 g. How many calories will contain the identical chocolate roller of a prism shape with a length of 0.5 m whose cross-section is an isosceles trapezoid with bases 25 and 13 cm and legs 10 cm? You know that 100 g of
The cube of 5 cm chocolate roll weighs 30 g. How many calories will contain the identical chocolate roller of a prism shape with a length of 0.5 m whose cross-section is an isosceles trapezoid with bases 25 and 13 cm and legs 10 cm? You know that 100 g of - Equilateral cone
 We pour so much water into a container with the shape of an equilateral cone, the base of which has a radius r = 6 cm, that one-third of the volume of the cone is filled. How high will the water reach if we turn the cone upside down?
We pour so much water into a container with the shape of an equilateral cone, the base of which has a radius r = 6 cm, that one-third of the volume of the cone is filled. How high will the water reach if we turn the cone upside down? - Pentagonal pyramid
 Find the volume and surface of a regular pentagonal pyramid with a base edge a = 12.8 cm and a height v = 32.1 cm.
Find the volume and surface of a regular pentagonal pyramid with a base edge a = 12.8 cm and a height v = 32.1 cm.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
