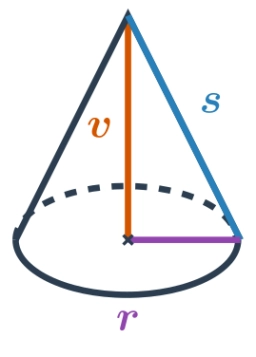
Equilateral cone

We pour so much water into a container with the shape of an equilateral cone, the base of which has a radius r = 6 cm, that one-third of the volume of the cone is filled. How high will the water reach if we turn the cone upside down?

Correct answer:

x = 1.3138 cm

Step-by-step explanation:

r = 6 cm s = d = 2 r s = 2 \cdot r = 2 \cdot 6 = 12 cm s^{2} = r^{2} + h^{2} h = s^{2} - r^{2} = 1 2^{2} - 6^{2} = 63 cm ≐ 10.3923 cm V = \frac{1}{3} \cdot π \cdot r^{2} \cdot h = \frac{1}{3} \cdot 3.1416 \cdot 6^{2} \cdot 10.3923 ≐ 391.7807 cm^{3} V_{1} = \frac{1}{3} \cdot V = \frac{1}{3} \cdot 391.7807 ≐ 130.5936 cm^{3} V_{2} = V - V_{1} = 391.7807 - 130.5936 ≐ 261.1871 cm^{3} V_{2} = \frac{1}{3} \cdot π \cdot r_{2}^{2} \cdot h_{2} r_{2} : h_{2} = r : h V_{2} = \frac{1}{3} \cdot π \cdot (r / h \cdot h_{2})^{2} \cdot h_{2} 3 \cdot V_{2} / π = r^{2} / h^{2} \cdot h_{2}^{2} \cdot h_{2} 3 \cdot V_{2} / π = r^{2} / h^{2} \cdot h_{2}^{3} h_{2} = 3 \frac{3 \cdot V _{2} \cdot h ^{2}}{π \cdot r ^{2}} = 3 \frac{3 \cdot 2 6 1 . 1 8 7 1 \cdot 1 0 . 3 9 2 3 ^{2}}{3 . 1 4 1 6 \cdot 6 ^{2}} ≐ 9.0785 cm x = h - h_{2} = 10.3923 - 9.0785 ≐ 1.3138 cm Verifying Solution: r_{2} = h_{2} \cdot r / h = 9.0785 \cdot 6 / 10.3923 ≐ 5.2415 cm V_{22} = \frac{1}{3} \cdot π \cdot r_{2}^{2} \cdot h_{2} = \frac{1}{3} \cdot 3.1416 \cdot 5.241 5^{2} \cdot 9.0785 ≐ 261.1871 cm^{3} V_{22} = V_{2} r_{1} : h_{1} = r : h V_{1} = \frac{1}{3} \cdot π \cdot r_{1}^{2} \cdot h_{1} V_{1} = \frac{1}{3} \cdot π \cdot r_{1}^{2} \cdot (r_{1} \cdot h / r) V_{1} = \frac{1}{3} \cdot π \cdot r_{1}^{3} \cdot (h / r) r_{1} = 3 3 \cdot V_{1} \cdot r / (π \cdot h) = 3 3 \cdot 130.5936 \cdot 6 / (3.1416 \cdot 10.3923) ≐ 4.1602 cm h_{1} = r_{1} \cdot h / r = 4.1602 \cdot 10.3923 / 6 ≐ 7.2056 cm V_{11} = \frac{1}{3} \cdot π \cdot r_{1}^{2} \cdot h_{1} = \frac{1}{3} \cdot 3.1416 \cdot 4.160 2^{2} \cdot 7.2056 ≐ 130.5936 cm^{3}

Did you find an error or inaccuracy? Feel free to write us. Thank you!

Showing 1 comment:

Aleksandra-maria

Dear Sirs! Considering English is not my mother tongue, I hope I understood the word problem as well as the solution you have provided (since there's no image in solution I hope that I understood the labels of the variables that you've uses in the solution) . .. Anyway, I think there is an error in the given solution. .. When you turn the cone upside down, the shape of the cone part filled with water is a truncated cone with the height h₂, so it's volume can not be calculated using formula that you have used, that is V₁=1/3 * pi * r² * h₂ . .. This isn't the formula for the volume of a truncated cone. ..

Best regards

4 years ago Like

Tips for related online calculators

Check out our ratio calculator.
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
See also our trigonometric triangle calculator.

You need to know the following knowledge to solve this word math problem:

Units of physical quantities:

volume

Grade of the word problem:

We encourage you to watch this tutorial video on this math problem: video1 video2