Rovnostranny kužel
Do nádoby tvaru rovnostranného kužele, jehož podstava má poloměr r = 6 cm nalijeme tolik vody, že se naplní jedna třetina objemu kužele. Do jaké výšky bude sahat voda, pokud kužel obrátíme dnem vzhůru?
Vaše odpověď:
Vaše odpověď:
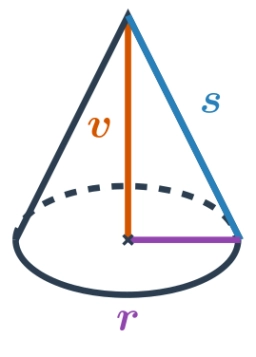
Tipy na související online kalkulačky
Vyzkoušejte naši kalkulačka na přepočet poměru.
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
geometriealgebraaritmetikastereometrieplanimetriezákladní operace a pojmyJednotky fyzikálních veličinÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Nálevka
Nálevka má tvar rovnostranného kužele. Vypočítejte obsah plochy smáčené vodou v případě, že do nálevky nalijeme 6,1 litry vody. - Do rotačního
Do rotačního kužele je vepsán válec, jehož výska je rovna polovině výšky kužele. Určete poměr objemů obou těles. - Objemový poměr
Vypočtěte poměr objemů kuliček opsané (poloměr r) a vepsaných (průměr ρ) do rovnostranného rotačního kužele. - Válec
V nádobě tvaru válce je 80 litrů vody. Voda sahá do výšky 45 cm. Kolik litrů vody bude v nádobě, bude - li sahat do výšky 72 cm? Výsledek zapiš v litrech, jednotky neuváděj, zapiš jen jako celé nebo desetinné číslo. - Výška vody v akváriu
Dno akvária má rozměry 30 cm a 50 cm. Do jaké výšky se akvárium naplní, pokud do něj naliji 60 litrů vody? - Kužel s průměrem
Nádoba tvaru kužele s průměrem dna 60 cm a boční stranou délky 0,5 m je zcela naplněna vodou. Vodu přelijeme do nádoby, která má tvář válce o poloměru 3 dm a výšce 20 cm. Bude válec přetékat, nebo naopak nebude plný? Vypočítejte kolik vody přeteče, nebo n - Valcová nádoba
Do válcové nádoby vlily 3,5 litru vody. Pokud měla nádoba průměr podstavy 3 dm, voda sahala přibližně do jaké výšky?
