Expression of a variable from the formula - math word problems - page 21 of 132
Number of problems found: 2638
- Binibini
 Binibini owns a triangular residential lot bounded by two roads intersecting at 70°. The sides of the lot along the road are 62m and 43m, respectively. Find the length of the fence needed to enclose the lot. (express answers to the nearest hundredths)
Binibini owns a triangular residential lot bounded by two roads intersecting at 70°. The sides of the lot along the road are 62m and 43m, respectively. Find the length of the fence needed to enclose the lot. (express answers to the nearest hundredths) - Perpendicular 73264
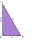 The perimeter of a right triangle is equal to 30 centimeters. Calculate the perpendicular b if a = 5 centimeters and c = 13 centimeters. A natural number expresses the length of the perpendicular b.
The perimeter of a right triangle is equal to 30 centimeters. Calculate the perpendicular b if a = 5 centimeters and c = 13 centimeters. A natural number expresses the length of the perpendicular b. - A flagpole
 A flagpole is leaning at an angle of 107° with the ground. A string fastened to the top of the flagpole is holding up the pole. The string makes an angle of 38° with the ground, and the flagpole is 8 m long. What is the length of the string?
A flagpole is leaning at an angle of 107° with the ground. A string fastened to the top of the flagpole is holding up the pole. The string makes an angle of 38° with the ground, and the flagpole is 8 m long. What is the length of the string? - Calculate 73024
 Calculate the permille descent of the railway line in the section of 7.2 km by 21.6 m.
Calculate the permille descent of the railway line in the section of 7.2 km by 21.6 m.
- Decimetres 72974
 What is the diameter of a 1m³ sphere? Write in decimetres
What is the diameter of a 1m³ sphere? Write in decimetres - A capacity
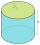 Suppose the cylinder at the right holds a capacity of 2 205 cm³ and its base area of 105 cm². How high is the cylinder?
Suppose the cylinder at the right holds a capacity of 2 205 cm³ and its base area of 105 cm². How high is the cylinder? - Z score transformation
 The annual salary of an entry-level statistics major (in thousands of dollars) is normally distributed with a mean of 75 and a standard deviation of 12. X ∼ N ( μ = 75, σ = 12 ). What is the minimum salary a statistics major should aim for in order to ear
The annual salary of an entry-level statistics major (in thousands of dollars) is normally distributed with a mean of 75 and a standard deviation of 12. X ∼ N ( μ = 75, σ = 12 ). What is the minimum salary a statistics major should aim for in order to ear - Indoor aquarium
 World's biggest indoor aquarium. In its enormous tank with the capacity represented by the following polynomial V=4x³+43x²+63x The aquarium is rectangular prism shape. Find the following: 1. If the aquarium's height is x, then find the area of the base (B
World's biggest indoor aquarium. In its enormous tank with the capacity represented by the following polynomial V=4x³+43x²+63x The aquarium is rectangular prism shape. Find the following: 1. If the aquarium's height is x, then find the area of the base (B - Casserole 72634
 The casserole with a volume of V = 4.5 l has a depth of h = 10 cm. Calculate its inside diameter.
The casserole with a volume of V = 4.5 l has a depth of h = 10 cm. Calculate its inside diameter.
- Calculate 72624
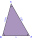 The perimeter of the ABC triangle is 19.6 cm. The following applies to the lengths of its sides: a: c = 1:2, b: c = 5:6. Calculate the lengths of all sides of the triangle ABC.
The perimeter of the ABC triangle is 19.6 cm. The following applies to the lengths of its sides: a: c = 1:2, b: c = 5:6. Calculate the lengths of all sides of the triangle ABC. - Arithmetic 72544
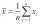 The arithmetic mean of two numbers is 12. The first number is 5. What is the value of the second number?
The arithmetic mean of two numbers is 12. The first number is 5. What is the value of the second number? - Centimeters 72534
 Calculate the edge c and the surface S of a block if its volume is equal to 42 cubic centimeters, a = 6cm, b = 3.5cm, c =?
Calculate the edge c and the surface S of a block if its volume is equal to 42 cubic centimeters, a = 6cm, b = 3.5cm, c =? - Hypotenuse 72524
 We know the height of the hypotenuse h = 4cm and the hypotenuse c = 19cm in a right triangle. How to calculate the segments of legs - sections on the hypotenuse c1, c2
We know the height of the hypotenuse h = 4cm and the hypotenuse c = 19cm in a right triangle. How to calculate the segments of legs - sections on the hypotenuse c1, c2 - Trapezoid 45
 Trapezoid with: Area: 345 1/2 sq cm base 1= 15 1/3 cm height= 4 1/5 cm What size has base 2?
Trapezoid with: Area: 345 1/2 sq cm base 1= 15 1/3 cm height= 4 1/5 cm What size has base 2?
- Circumference 72414
 Calculate the diagonal and the area of a square if its circumference is 10 centimeters.
Calculate the diagonal and the area of a square if its circumference is 10 centimeters. - Surface 72394
 The volume of the cube is 15625 cubic meters. Find the length of the edge and the surface of the cube.
The volume of the cube is 15625 cubic meters. Find the length of the edge and the surface of the cube. - Evaluate 25
 Evaluate the following expression: [ 3 + ( 40 ÷ 5 ) x ( 2 x 2 ) ] – 5 =
Evaluate the following expression: [ 3 + ( 40 ÷ 5 ) x ( 2 x 2 ) ] – 5 = - Length and width
 Use the 5-step procedure. The perimeter of a rectangle is 34 in. The length is 4 in less than three times the width. Find the length and width.
Use the 5-step procedure. The perimeter of a rectangle is 34 in. The length is 4 in less than three times the width. Find the length and width. - A hiker
 A hiker plans to hike up one side of a mountain and down the other side of points a mountain, each side of the mountain formed by a straight line. The angle of elevation at the starting point is 42.4 degrees, and the angle of elevation at the end is 48.3
A hiker plans to hike up one side of a mountain and down the other side of points a mountain, each side of the mountain formed by a straight line. The angle of elevation at the starting point is 42.4 degrees, and the angle of elevation at the end is 48.3
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
