Hypotenuse 72524
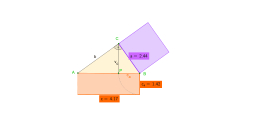
We know the height of the hypotenuse h = 4cm and the hypotenuse c = 19cm in a right triangle. How to calculate the segments of legs - sections on the hypotenuse c1, c2
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
The Pythagorean theorem is the base for the right triangle calculator.
Do you want to convert time units like minutes to seconds?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
The Pythagorean theorem is the base for the right triangle calculator.
Do you want to convert time units like minutes to seconds?
You need to know the following knowledge to solve this word math problem:
algebraarithmeticplanimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Right-angled 82471
The lengths a = 7.2 cm and b = 10.4 cm are dropped in the right-angled triangle ABC. Do the math a) lengths of the sections of the hypotenuse b) height on the hypotenuse c - Euclid1
The right triangle ABC has hypotenuse c = 20 cm. How large sections cut height hc=9 cm on the hypotenuse c? - Right triangle ABC
Calculate the perimeter and area of a right triangle ABC. If you know the length of the legs, 4 cm, 5.5 cm, and 6.8 cm are the hypotenuse. - Trapezoid ABCD
Calculate the perimeter of trapezoid ABCD if we know the side c=12, b=19, which is also a height, and side d=32.
- Segments on the hypotenuse
A right triangle ABC has a hypotenuse of c=26cm. How many segments does the height vc=12 cm cut out on the hypotenuse c? What are the lengths of the sides a and b? What are the angles at the vertices A and B? - Hypotenuse and height
In a right triangle is length of the hypotenuse c = 195 cm and height hc = 70 cm. Determine the length of both triangle legs. - RT triangle and height
Calculate the remaining sides of the right triangle if we know side b = 4 cm long and height to side c h = 2.4 cm.
