Diameter
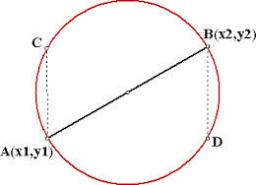
If the endpoints of the diameter of a circle are A(10, -10) and
B (9, -2), what is the circle's radius?
B (9, -2), what is the circle's radius?
Final Answer:
Tips for related online calculators
The Pythagorean theorem is the base for the right triangle calculator.
You need to know the following knowledge to solve this word math problem:
geometryarithmeticplanimetricsGrade of the word problem
Related math problems and questions:
- Different circles
Draw five circles with different radii. Measure the diameter of each circle and compare it to its radius. What is true about them? - Quadrilateral circle radius
Given is a quadrilateral ABCD inscribed in a circle, with the diagonal AC being the circle's diameter. The distance between point B and the diameter is 15 cm, and between point D and the diameter is 18 cm. Calculate the radius of the circle and the perime - Circle radius
The area of the two circles is in a 4:9 ratio. The larger circle has a diameter of 12 cm. Calculate the radius of the smaller circle. - Chord
The point on the circle is the endpoint of diameter and endpoint of the chord length of the radius. What angle between chord and diameter? - Circle radius calculation
The area of the two circles is in a 4:9 ratio. The larger circle has a diameter of 18 cm. Calculate the radius of the smaller circle. - Circle radius calculation
Point B is the center of the circle. The line AC touches the circles at point C and applies AB = 20 cm and AC = 16 cm. What is the radius of the circle BC? - Tangent 3
In a circle with a center O radius is 4√5 cm. EC is the tangent to the circle at point D. Segment AB is a given circle's DIAMETER. POINT A is joined with POINT E, and POINT B is joined with POINT C. Find DC if BC IS 8cm.
