Euclidean distance
Calculate the Euclidean distance between shops A, B, and C, where:
A 45 0.05
B 60 0.05
C 52 0.09
The first figure is the weight in grams of bread, and the second figure is the USD price.
A 45 0.05
B 60 0.05
C 52 0.09
The first figure is the weight in grams of bread, and the second figure is the USD price.
Correct answer:
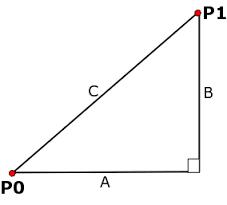
Tips for related online calculators
The Pythagorean theorem is the base for the right triangle calculator.
You need to know the following knowledge to solve this word math problem:
planimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Calculate 55803
Calculate the weight of 2.00 moles of common salt (NaCl) in grams. M (NaCl) = 55.44 g / mol. - Salami
We have six kinds of salami, six of which have ten pieces, and one of which has four pieces. How many ways can we distinctly choose five pieces of salami? - A sample
A sample of 10 randomly selected students revealed the following grades in Business Statistics first test (on a marking scale of 0 to 100): 79, 63, 60, 45, 55, 58, 59, 62, 40, 68. Examine the data using groups and presenting: a) the Histogram of the absol - Grams and kilos
1. Tunji weighs 67 kg 114 g, while Deji weighs 54kg 596g. What is the sum total of their weight? 2. Adamu is 2kg 324g lighter than Muazu; if Muazu weighs 49kg 158g, what is Adamu's weight? - Z-score
The mean adult male pulse rate is 67.3 beats per minute, with a standard deviation of 10.3. Find the z-score for an adult male's pulse rate of 75. (Round the z-score to two decimal places. ) - Spruce wood
Calculate the weight of an edge made of spruce wood 6m long when the cross-section of the edge is 146cm square and if the density of the wood is 0.55 grams/cm cubic. - Trains
On a double-track line between stations, K and M went against each other two trains. The first train passed the distance between stations for 1 hours, and the second, which had an average speed of 11 km/h more, passed for 0.65 hours. Calculate the distanc
