Angled cyclist turn
The cyclist passes through a curve with a radius of 20 m at 25 km/h. How much angle does it have to bend from the vertical inward to the turn?
Correct answer:
Showing 1 comment:
Matematik
A cyclist has to bend slightly towards the center of the circular track in order to make a safe turn without slipping.
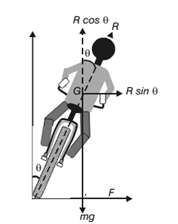
Let m be the mass of the cyclist along with the bicycle and v, the velocity. When the cyclist negotiates the curve, he bends inwards from the vertical, by an angle θ. Let R be the reaction of the ground on the cyclist. The reaction R may be resolved into two components:
(i) the component R sin θ, acting towards the center of the curve providing necessary centripetal force for circular motion and
(ii) the component R cos θ, balancing the weight of the cyclist along with the bicycle.
Thus for less bending of the cyclist (i.e for θ to be small), the velocity v should be smaller and radius r should be larger. let h be the elevation of the outer edge of the road above the inner
edge and l be the width of the road then,
Let m be the mass of the cyclist along with the bicycle and v, the velocity. When the cyclist negotiates the curve, he bends inwards from the vertical, by an angle θ. Let R be the reaction of the ground on the cyclist. The reaction R may be resolved into two components:
(i) the component R sin θ, acting towards the center of the curve providing necessary centripetal force for circular motion and
(ii) the component R cos θ, balancing the weight of the cyclist along with the bicycle.
Thus for less bending of the cyclist (i.e for θ to be small), the velocity v should be smaller and radius r should be larger. let h be the elevation of the outer edge of the road above the inner
edge and l be the width of the road then,
Tips for related online calculators
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Do you want to convert mass units?
Do you want to convert velocity (speed) units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Do you want to convert mass units?
Do you want to convert velocity (speed) units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
- geometry
- vector
- algebra
- equation
- expression of a variable from the formula
- planimetrics
- right triangle
- triangle
Units of physical quantities:
Themes, topics:
Grade of the word problem:
Related math problems and questions:
- Horizontal 83148
The bend has a radius of r = 100 m and is inclined at an angle of 20° to the horizontal plane (= tilt angle). What is the safe (the "best") speed to go through this curve? Sketch the picture regarding NIVS, mark the forces, and calculate. - Rail turn
The curve radius on the railway line is 532 m. The length of the rail track on it is 818 m. How many degrees is the angle ASB if A and B are boundary points and S is the center of the arc curve? - The bridge
A vehicle weighing 5,800 kg passes 41 km/h on an arched bridge with a radius of curvature of 62 m. What force pushes the car onto the bridge as it passes through the center? What maximum speed can it cross over the bridge's center so it does not fly off t - Coordinates 21553
I have to calculate the basis of the exponential function f: A on x. The function passes through point A with coordinates (-2, twenty-five quarters).
- Resistance 25031
The current of 25 mA passes through the resistor with a resistance of 50Ω. How much voltage do we measure on it? - Traveling 6067
A car traveling at 75 km/h will drive from place A to place B in 3/4 hours. How long does it take for a cyclist to get there at a speed of 25 km/h? - Cyclist and car
A cyclist who runs at a speed of 20km per hour will arrive at the finish in 4.5 hours. How fast does the car have to drive the same route in 2 hours?
