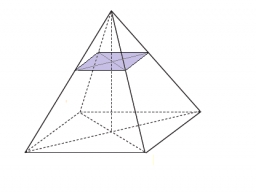
Quadrilateral pyramid
In a regular quadrilateral pyramid, the side edge is e = 7 dm, and the diagonal of the base is 50 cm. Calculate the pyramid shell area.
Correct answer:
Tips for related online calculators
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- solid geometry
- pyramid
- surface area
- planimetrics
- polygon
- area of a shape
- triangle
- square
- diagonal
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- ET inscribed circle
 An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region.
An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region. - The triangle 6
 The triangle has an area of 7 ⅞ cm² and a base of 5 ¼ cm. What is the length of h? Explain your reasoning.
The triangle has an area of 7 ⅞ cm² and a base of 5 ¼ cm. What is the length of h? Explain your reasoning. - Quadrilateral 82616
 Triangle ABC is divided into line segments. Lines DE and AB are parallel. Triangles CDH, CHI, CIE, and FIH have the same area, namely 8 dm². Find the content of quadrilateral AFHD.
Triangle ABC is divided into line segments. Lines DE and AB are parallel. Triangles CDH, CHI, CIE, and FIH have the same area, namely 8 dm². Find the content of quadrilateral AFHD. - Panting
 If the base of the triangle is 2 3/4 meters & and the altitude is 3 2/3 meters, then what is the cost of panting on both sides at ₹3 1/2 per sq.m.?
If the base of the triangle is 2 3/4 meters & and the altitude is 3 2/3 meters, then what is the cost of panting on both sides at ₹3 1/2 per sq.m.?
- Januka
 Januka and her father were going to the tent. They found that their old tent was torn. Their mother suggested that they sew a tent whose walls would be made of 4 identical isosceles triangles. Their lower side is 2 m long, and the height is also 2 m. Then
Januka and her father were going to the tent. They found that their old tent was torn. Their mother suggested that they sew a tent whose walls would be made of 4 identical isosceles triangles. Their lower side is 2 m long, and the height is also 2 m. Then - Area - simple
 Find the area of the triangle. So, the base is 7 2/3 mi. The height is 7 mi. What is the Area?
Find the area of the triangle. So, the base is 7 2/3 mi. The height is 7 mi. What is the Area? - Storage shed
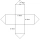 Frank designed a net for a storage shed that he is going to construct out of metal. The design consists of a square base and four square sides, plus four triangular parts that make up the roof. A square base of 6 feet and four square sides, plus 4 feet of
Frank designed a net for a storage shed that he is going to construct out of metal. The design consists of a square base and four square sides, plus four triangular parts that make up the roof. A square base of 6 feet and four square sides, plus 4 feet of - The volume 8
 The volume of a right regular hexagonal prism is 187.2 cubic millimeters. The line segment that has a length of 2.6 millimeters begins at the center of the hexagon and ends at one side of the hexagon. 3 mm base. Find the height.
The volume of a right regular hexagonal prism is 187.2 cubic millimeters. The line segment that has a length of 2.6 millimeters begins at the center of the hexagon and ends at one side of the hexagon. 3 mm base. Find the height. - A triangle 9
 A triangle has an area of 16 1/2 square units. The height is 3 2/3. What is the base?
A triangle has an area of 16 1/2 square units. The height is 3 2/3. What is the base?
- Felix
 Calculate how much land Felix Baumgartner saw after jumping from 36 km above the ground. The radius of the Earth is R = 6378 km.
Calculate how much land Felix Baumgartner saw after jumping from 36 km above the ground. The radius of the Earth is R = 6378 km. - Isosceles triangle
 Find the area of an isosceles triangle whose leg is twice the base, b=1
Find the area of an isosceles triangle whose leg is twice the base, b=1 - ABS, ARG, CONJ, RECIPROCAL
 Let z=-√2-√2i where i2 = -1. Find |z|, arg(z), z* (where * indicates the complex conjugate), and (1/z). Where appropriate, write your answers in the form a + i b, where both a and b are real numbers. Indicate the positions of z, z*, and (1/z) on an Argand
Let z=-√2-√2i where i2 = -1. Find |z|, arg(z), z* (where * indicates the complex conjugate), and (1/z). Where appropriate, write your answers in the form a + i b, where both a and b are real numbers. Indicate the positions of z, z*, and (1/z) on an Argand - Isosceles right triangle
 If the square of the hypotenuse of an isosceles right triangle is 128 cm2, find the length of each side.
If the square of the hypotenuse of an isosceles right triangle is 128 cm2, find the length of each side. - Triangle 73464
 The given line is a BC length of 6 cm. Construct a triangle so that the BAC angle is 50° and the height to the side is 5.5 cm. Thank you very much.
The given line is a BC length of 6 cm. Construct a triangle so that the BAC angle is 50° and the height to the side is 5.5 cm. Thank you very much.
- An equivalent
 An equilateral triangle has the same perimeter as a rectangle whose sides are b and h (b > h). Considering that the area of the triangle is three times the area of the rectangle. What is the value of b/h?
An equilateral triangle has the same perimeter as a rectangle whose sides are b and h (b > h). Considering that the area of the triangle is three times the area of the rectangle. What is the value of b/h? - An isosceles
 An isosceles trapezoid has base angles of 50° each, and its bases are 20 cm and 30 cm. Compute its area.
An isosceles trapezoid has base angles of 50° each, and its bases are 20 cm and 30 cm. Compute its area. - Deviation 70434
 Frustum has the base radii of the figures r1 and r2: r1> r2, r2 = s, and if the side deviation from the base plane is 60°. Express the surface and volume of the cone frustum using its side s.
Frustum has the base radii of the figures r1 and r2: r1> r2, r2 = s, and if the side deviation from the base plane is 60°. Express the surface and volume of the cone frustum using its side s.
