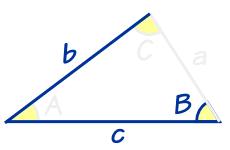
Rhomboid
The rhomboid sides' dimensions are a= |AB|=5 cm, b = |BC|=6 cm, and the angle's size at vertex A is 60°. What is the length of the diagonal AC?
Final Answer:
Tips for related online calculators
Do you want to convert length units?
The Pythagorean theorem is the base for the right triangle calculator.
Do you want to convert time units like minutes to seconds?
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
The Pythagorean theorem is the base for the right triangle calculator.
Do you want to convert time units like minutes to seconds?
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
arithmeticplanimetricsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Quadrilateral triangle segment
The quadrilateral ABCD is symmetrical about the diagonal AC. The length of AC is 12 cm, the length of BC is 6 cm, and the interior angle at vertex B is right. points E and F are given on the sides AB, and AD so that the triangle ECF is equilateral. Determ - Triangle in a square
In a square ABCD with side a = 6 cm, point E is the center of side AB, and point F is the center of side BC. Calculate the size of all angles of the triangle DEF and the lengths of its sides. - Draw triangle
Construct an isosceles triangle ABC, if AB = 7cm, the size of the angle ABC is 47°, arms | AC | = | BC |. Measure the size of the BC side in mm. - The right triangle
In the right triangle ABC with a right angle at C, we know the side lengths AC = 9 cm and BC = 7 cm. Calculate the length of the remaining side of the triangle and the size of all angles. - MO Z7–I–6 2021
In triangle ABC, point D lies on the AC side and point E on the BC side. The sizes of the angles ABD, BAE, CAE, and CBD are 30°, 60°, 20°, and 30°, respectively. Find the size of the AED angle. - Parallelogram - diagonals
Suppose a parallelogram ABCD, the length of one of its diagonals is equal to that of one of its sides. What are the interior angles of this parallelogram? - ABCD rhombus
ABCD is a rhombus with sides 10.5cm. If the length of the diagonal AC=15.8cm, using cosine formula. a. calculate the length of the diagonal BD correct to the nearest cm b. the angles of the rhombus to the nearest degree.
