MO - triangles
On the AB and AC sides of the ABC triangle lies successive points E and F, and on segment EF lie point D. The EF and BC lines are parallel. It is true this ratio FD:DE = AE:EB = 2:1. The area of the ABC triangle is 27 hectares, and line segments EF, AD, and DB segments are divided into four parts. Find the areas of these four parts.
Correct answer:

Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Themes, topics:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Circumferences 83111
 Péta composed several planar shapes from mutually congruent triangles. The circumferences of the first three are 8 cm, 11.4 cm, and 14.7 cm, respectively. Determine the perimeter of the fourth shape.
Péta composed several planar shapes from mutually congruent triangles. The circumferences of the first three are 8 cm, 11.4 cm, and 14.7 cm, respectively. Determine the perimeter of the fourth shape. - Quadrilateral 82616
 Triangle ABC is divided into line segments. Lines DE and AB are parallel. Triangles CDH, CHI, CIE, and FIH have the same area, namely 8 dm². Find the content of quadrilateral AFHD.
Triangle ABC is divided into line segments. Lines DE and AB are parallel. Triangles CDH, CHI, CIE, and FIH have the same area, namely 8 dm². Find the content of quadrilateral AFHD. - Two-digit 82521
 Karel had to multiply two two-digit numbers. Out of care, he changed the order of the digits in one of the factors and got a product that was 4,248 less than the correct result. What is the correct result? How much should Karl have earned?
Karel had to multiply two two-digit numbers. Out of care, he changed the order of the digits in one of the factors and got a product that was 4,248 less than the correct result. What is the correct result? How much should Karl have earned? - Department 82388
 Last year, there were 30 more boys than girls in our scout troop. This year, the number of children in the ward increased by 10%, while the number of boys increased by 5% and the number of girls increased by 20%. How many children do we have in the depart
Last year, there were 30 more boys than girls in our scout troop. This year, the number of children in the ward increased by 10%, while the number of boys increased by 5% and the number of girls increased by 20%. How many children do we have in the depart
- Quadrilateral calc
 The square ABCD is given. The midpoint of AB is E, the midpoint of BC is F, CD is G, and the midpoint of DA is H. Join AF, BG, CH, and DE. Inside the square (approximately in the middle), the intersections of these line segments form a quadrilateral. Calc
The square ABCD is given. The midpoint of AB is E, the midpoint of BC is F, CD is G, and the midpoint of DA is H. Join AF, BG, CH, and DE. Inside the square (approximately in the middle), the intersections of these line segments form a quadrilateral. Calc - SKMO
 Petra had written natural numbers from 1 to 9. She added two of these numbers, deleted them, and wrote the resulting sum instead of the summaries. She thus had eight numbers written down, which she managed to divide into two groups with the same product.
Petra had written natural numbers from 1 to 9. She added two of these numbers, deleted them, and wrote the resulting sum instead of the summaries. She thus had eight numbers written down, which she managed to divide into two groups with the same product. - Grandchildren 80639
 The average age of the grandfather, grandmother, and their five grandchildren is 26 years. The average age of the grandchildren themselves is 7 years. Grandma is a year younger than grandpa. How old is grandma?
The average age of the grandfather, grandmother, and their five grandchildren is 26 years. The average age of the grandchildren themselves is 7 years. Grandma is a year younger than grandpa. How old is grandma? - Smallest z9
 Find the smallest positive numbers a and b for which 7a³ = 11b⁵
Find the smallest positive numbers a and b for which 7a³ = 11b⁵ - Positive integer integral
 How many different sets of a positive integer in the form (x, y, z) satisfy the equation xyz=1400?
How many different sets of a positive integer in the form (x, y, z) satisfy the equation xyz=1400?
- Two-digit 64294
 How many natural two-digit numbers can we form from the digits 0, 1, 2, and 3 if the numerals cannot be repeated in these numbers?
How many natural two-digit numbers can we form from the digits 0, 1, 2, and 3 if the numerals cannot be repeated in these numbers? - Book Store
 The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w
The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w - Mr. Product
 The product of ages of all of Mr. Product's children is 1408. The age of the youngest child is equal to half the age of the oldest child. How many children does Mr. Product have, and how old are they?
The product of ages of all of Mr. Product's children is 1408. The age of the youngest child is equal to half the age of the oldest child. How many children does Mr. Product have, and how old are they? - Three-digit unknown int
 Viera compiled different three-digit numbers from three given digits. When she added up all these numbers, she published 1221. What numbers did Vierka use? Identify five options
Viera compiled different three-digit numbers from three given digits. When she added up all these numbers, she published 1221. What numbers did Vierka use? Identify five options - MO Z7–I–6 2021
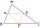
 In triangle ABC, point D lies on the AC side and point E on the BC side. The sizes of the angles ABD, BAE, CAE, and CBD are 30°, 60°, 20°, and 30°, respectively. Find the size of the AED angle.
In triangle ABC, point D lies on the AC side and point E on the BC side. The sizes of the angles ABD, BAE, CAE, and CBD are 30°, 60°, 20°, and 30°, respectively. Find the size of the AED angle.
- Two ports
 Between the ports of Mumraj and Zmatek, two ships commute along the same route. They spend negligible time in ports, turn around immediately, and continue sailing. At the same time, a blue ship departs from the port of Mumraj, and a green ship departs fro
Between the ports of Mumraj and Zmatek, two ships commute along the same route. They spend negligible time in ports, turn around immediately, and continue sailing. At the same time, a blue ship departs from the port of Mumraj, and a green ship departs fro - Coloured numbers
 Mussel wrote four different natural numbers with colored markers: red, blue, green, and yellow. When the red number divides by blue, it gets the green number as an incomplete proportion, and yellow represents the remainder after this division. When it div
Mussel wrote four different natural numbers with colored markers: red, blue, green, and yellow. When the red number divides by blue, it gets the green number as an incomplete proportion, and yellow represents the remainder after this division. When it div - Squirrels
 The squirrels discovered a bush with hazelnuts. The first squirrel plucked one nut, the second squirrel two nuts, and the third squirrel three nuts. Each new squirrel always tore one nut more than the previous squirrel. When they plucked all the nuts from
The squirrels discovered a bush with hazelnuts. The first squirrel plucked one nut, the second squirrel two nuts, and the third squirrel three nuts. Each new squirrel always tore one nut more than the previous squirrel. When they plucked all the nuts from
