Circle - AG
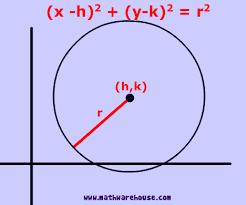
Find the coordinates of the circle and its diameter if its equation is:
x2+y2−6x−4y=36
Your answer:
x2+y2−6x−4y=36
Your answer:
Tips for related online calculators
The Pythagorean theorem is the base for the right triangle calculator.
You need to know the following knowledge to solve this word math problem:
geometryalgebraplanimetryGrade of the word problem
Related math problems and questions:
- Vertex of the rectangle
Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0 - Circle
The circle touches two parallel lines, p, and q, and its center lies on line a, which is the secant of lines p and q. Write the equation of the circle and determine the coordinates of the center and radius. p: x-10 = 0 q: -x-19 = 0 a: 9x-4y+5 = 0 - Find parameters
Find parameters of the circle in the plane - coordinates of center and radius: x²+(y-3)²=14 - Find midpoint
FM=5y+13, MG=5-3y, FG=? M is the midpoint of FG. Use the given information to find the missing measure or value. - Circle length center
Calculate the circle's length and determine the coordinates of the center of the circle when given its diameter XY, X / -3.2 / and Y / -3, -4 /. - Circle
From the equation of a circle: -x² -y² +16x -4y -59 = 0 Calculate the coordinates of the centre S[x₀, y₀] and the radius r of the circle. - Intersection of functions
Draw a graph of the function given by the equation y = -2x +3, find its intersections with the coordinate axes, and complete the unknown coordinates A [3;? ], B [?; 8].
