Find parameters
Find parameters of the circle in the plane - coordinates of center and radius:
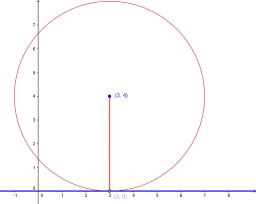
x2+(y−3)2=14
x2+(y−3)2=14
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Circle
From the equation of a circle: -x² -y² +16x -4y -59 = 0 Calculate the coordinates of the center of the circle S[x0, y0] and the radius of the circle r. - Circle
The circle touches two parallel lines, p, and q, and its center lies on line a, which is the secant of lines p and q. Write the equation of the circle and determine the coordinates of the center and radius. p: x-10 = 0 q: -x-19 = 0 a: 9x-4y+5 = 0 - Center
Calculate the coordinates of the circle center: x² -4x + y² +10y +25 = 0 - Circle - AG
Find the coordinates of the circle and its diameter if its equation is: x² + y² - 6x-4y=36
- Equation of the circle
Find the equation of the circle with the center at (1,20), which touches the line 8x+5y-19=0 - Sphere cuts
At what distance from the center does the sphere intersect with the radius R = 91 plane if the cut area and area of the main sphere circle are in ratio 3/6? - Ellipse
Ellipse is expressed by equation 9x² + 25y² - 54x - 100y - 44 = 0. Find the length of primary and secondary axes, eccentricity, and coordinates of the ellipse's center.
