Kruh v rovině
Najděte parametry kruhu v rovině - souřadnice středu a poloměr:
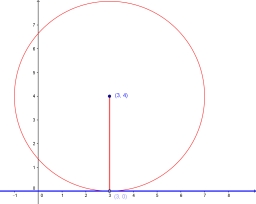
x2+(y−3)2=14
x2+(y−3)2=14
Správná odpověď:
Tipy na související online kalkulačky
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
geometriealgebraaritmetikaplanimetrieÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Souřadnice středu
Najděte souřadnice středu kruhu a jeho průměr, pokud jeho rovnice je: x² + y² - 6x-4y=36 - Kružnice
Z rovnice kružnice: 3x² +3y² +54x +168 = 0 Vypočítejte souřadnice středu kružnice S [x0, y0] a poloměr kružnice r. - Poloměr
Najděte poloměr kruhu pomocí Pythagorovy věty jestliže a = 9, b = r, c = 6 + r - Trojúhelník 32183
V rovině je dán trojúhelník ABC. A(-3,5), B(2,3), C(-1,-2) zapište souřadnice vektorů u, v, w pokud u=AB, v=AC, w=BC. Zapište souřadnice středů úseček SAB(. .), SAC(. .. ), SBC(. .. ) - Kružnice
Kružnice se dotýká dvou rovnoběžek p a q, její střed leží na přímce a, která je sečnou obou přímek. Napište její rovnici a určete souřadnice středu a poloměru. p: -5x-y-1 = 0 q: -5x-y+7 = 0 a: -2x+5y-6 = 0 - Souřadnice 74874
Rovnice křivky C je y = 2x2 - 8x +9 a rovnice přímky L je x + y = 3. (1) Najděte x-ové souřadnice průsečíků L a C. ii) ukázat, že jeden z těchto bodů je také - Koule
Najděte rovnici koule pokud na povrchu koule leží tři body (a, 0,0), (0, a, 0), (0,0, a) a střed leží na rovině x + y + z = a.
