Symmetry
Eva loves symmetry in shapes and numbers. Yesterday she invented an entirely new kind of symmetry - divisible symmetry. She wrote all five-digit numbers with different digits with the following property:
The first digit is divisible by 1, the second by 2, the third by 3, the fourth by four, and the fifth by 5, regardless of whether the digit reads from left to right or right to left.
List all five-digit numbers with Eva's divisible symmetry. How many are there?
The first digit is divisible by 1, the second by 2, the third by 3, the fourth by four, and the fifth by 5, regardless of whether the digit reads from left to right or right to left.
List all five-digit numbers with Eva's divisible symmetry. How many are there?
Correct answer:
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Four-digit numbers
Find four-digit numbers where all the digits are different. For numbers, the sum of the third and fourth digits is twice the sum of the first two digits, and the sum of the first and fourth digits is equal to the sum of the second and third digits. The di - Seven-segmet
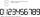Lenka is amused that he punched a calculator (seven-segment display) number and used only digits 2 to 9. Some numbers have the property that She again gave their image in the axial or central symmetry some number. Determine the maximum number of three-dig - Education - 5 modules
In a self-paced online class, there are five modules. The first four modules are worth the same, but the fifth module is worth as much as the other four combined. A student is one-fourth of the way through the last module and has done one-third of three o - Z9-I-4
Kate thought of a five-digit integer. She wrote the sum of this number and its half in the first line of the workbook. On the second line, write a total of this number, and its one fifth. She wrote a sum of this number and its one nines on the third row. - Three-digit 5524
Six cards with digits 1, 2, 3, 4, 5, and 6 are on the table. Agnes made a six-digit number from these cards, divisible by six. Then she gradually removed the cards from the right. A five-digit number divisible by five remained on the table when she remove - Characters 82998
Adam wrote the following sum with five secret adders: a + bb + ccc + dddd + eeeee. He revealed that the characters "a, b, c, d, e" represent the different digits 1, 2, 3, 4, and 5 and that the resulting sum is divisible by 11. Which is the smallest and wh - The missing digit
Complete the missing digit in the number 3 ∗ 43 to form a number divisible by three. If there are multiple options, list them all. (The omitted digit is marked with the symbol ∗. ) Answers must be justified! - Divisible by five
How many different three-digit numbers divisible by five can we create from the digits 2, 4, and 5? We can repeat the digits in the created number. - Five-digit number
Anna thinks of a five-digit number not divisible by three or four. If he increments each digit by one, it gets a five-digit number divisible by three. If he reduces each digit by one, he gets a five-digit number divisible by four. If it swaps any two digi - Unknown number
An unknown number is divisible by exactly three different primes. When we compare these primes in ascending order, the following applies: • Difference between the first and second prime numbers is half the difference between the third and second prime num - Five-digit 80104
How many different five-digit numbers with different digits can be made from the digits 0, 2, 4, 6, 7, 8, and 9? How many of them are divisible by 4? How many of them are divisible by 10? How many of them are even? - Three-digit 45361 How many different three-digit numbers divisible by five can we create from the digits 2, 4, and 5? The numerals can be repeated in the created number.
- PIN code
The PIN on Michael's credit card is a four-digit number. Michael told his friend: • It is a prime number - a number greater than 1, which is only divisible by number one and by itself. • The first digit is larger than the second. • The second digit is gre - Three-digit 7248
Find all three-digit numbers n with three different non-zero digits divisible by the sum of all three two-digit numbers we get when we delete one digit in the original number. - Three digits number
From the numbers 1, 2, 3, 4, and 5, create three-digit numbers whose digits do not repeat, and the number is divisible by 2. How many numbers are there? - Combinations
How many different combinations of two-digit number divisible by four arises from the digits 3, 5, and 7? - Preparation 73954
Ivana was preparing for Testing 9. On the first day, she calculated a quarter of all calculated tasks; on the second day, a sixth; on the third, a fifth; on the fourth, only an eighth; and on the last day, she solved 31 tasks. How many tasks did she recal
