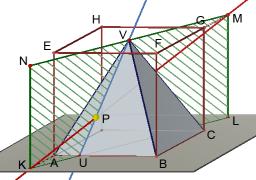
Regular quadrangular pyramid
The height of the regular quadrangular pyramid is 6 cm, the length of the base is 4 cm. What is the angle between the ABV and BCV planes?
Correct answer:
Tips for related online calculators
Do you want to convert length units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- solid geometry
- pyramid
- planimetrics
- right triangle
- triangle
- goniometry and trigonometry
- sine
- cosine
- tangent
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Pyramid
Pyramid has a base a = 3cm and height in v = 15 cm. a) calculate angle between plane ABV and base plane b) calculate angle between opposite side edges. - Quadrangular pyramid
Calculate the surface area and volume of a regular quadrangular pyramid: sides of bases (bottom, top): a1 = 18 cm, a2 = 6cm angle α = 60 ° (Angle α is the angle between the sidewall and the base plane.) S =? , V =? - Angle of two lines
There is a regular quadrangular pyramid ABCDV; | AB | = 4 cm; height v = 6 cm. Determine the angles of lines AD and BV. - Pyramid 4sides
Calculate the volume and the surface of a regular quadrangular pyramid when the edge of the base is 4 cm long and the height of the pyramid is 7 cm. - Pyramid - angle
Calculate the regular quadrangular pyramid's surface whose base edge measured 6 cm, and the deviation from the plane of the base's sidewall plane is 50 degrees. - Quadrangular pyramid
Given is a regular quadrangular pyramid with a square base. The body height is 30 cm and volume V = 1000 cm³. Calculate its side a and its surface area. - Quadrangular pyramid
The regular quadrangular pyramid has a base length of 6 cm and a side edge length of 9 centimeters. Calculate its volume and surface area. - Pentagonal pyramid
Calculate the volume of a regular 5-side (pentaprism) pyramid ABCDEV; if |AB| = 7.7 cm and a plane ABV, ABC has angle 37 degrees. - Four sided prism
Calculate the volume and surface area of a regular quadrangular prism whose height is 28.6cm and the body diagonal forms a 50-degree angle with the base plane. - Quadrilateral 8120
Include the side edge length of a regular quadrilateral pyramid if the pyramid height is 4 cm and the base area is 16 cm². - Pyramid 8 Calculate the volume and the surface area of a regular quadrangular pyramid with the base side 9 cm and side wall with the base has an angle 75°.
- Calculate 8354 In a regular pyramid in which the edge of the base is | AB | = 4cm; height = 6cm, calculate the angle of the lines AV and CV, V = vertex.
- Wall height
Calculate the surface and volume of a regular quadrangular pyramid if side a = 6 cm and wall height v = 0.8dm. - Quadrilateral pyramid
In a regular quadrilateral pyramid, the height is 6.5 cm and the angle between the base and the side wall is 42°. Calculate the surface area and volume of the body. Round calculations to 1 decimal place. - Roof 7
The roof has the shape of a regular quadrangular pyramid with a base edge of 12 m and a height of 4 m. How many percent is folds and waste if in construction was consumed 181.4m² of plate? - Quadrilateral 28491
Calculate the weight of a regular quadrilateral pyramid with a base edge of 4 cm in length and a body height of 6 cm if it is made of a material density of 8 g/cm³. - Pyramid of Giza
The Great Pyramid of Giza has the shape of a regular quadrangular pyramid. The base edge is 227 m long and 140 m high. What is the weight of the stone needed to build this pyramid, if the weight of 1 m³ of stone is 2.5 t?
