Recursion squares
In the square, ABCD has inscribed a square so that its vertices lie at the centers of the sides of the square ABCD. The procedure of inscribing the square is repeated this way. The side length of the square ABCD is a = 16 cm.
Calculate:
a) the sum of perimeters of all squares
b) the sum of the area of all squares
Calculate:
a) the sum of perimeters of all squares
b) the sum of the area of all squares
Correct answer:

Tips for related online calculators
See also our right triangle calculator.
Do you want to convert length units?
See also our trigonometric triangle calculator.
Do you want to convert length units?
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- geometric progression
- infinite geometric series
- arithmetic
- addition
- planimetrics
- Pythagorean theorem
- right triangle
- area of a shape
- perimeter
- triangle
- square
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Triangular 81985
 Trainees stand on the marks in rows exactly 1.5 m apart. They form an expanding triangular wedge (in each subsequent row, there is one more exerciser), while the distance between the front exerciser and the back row is 30 m. Determine the number of traine
Trainees stand on the marks in rows exactly 1.5 m apart. They form an expanding triangular wedge (in each subsequent row, there is one more exerciser), while the distance between the front exerciser and the back row is 30 m. Determine the number of traine - Geometric series
 How many terms of the geometric series 8+4+2+1+0.5+... must be taken for the sum to get within 10 to the power minus 4 of its sum to infinity?
How many terms of the geometric series 8+4+2+1+0.5+... must be taken for the sum to get within 10 to the power minus 4 of its sum to infinity? - Infinite sum of areas
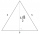 An equilateral triangle A1B1C1 is constructed above the height of the equilateral triangle ABC is constructed as. Above the height of the equilateral triangle A1B1C1 is built triangle A2B2C2, and so on. The procedure is repeated continuously. What is the
An equilateral triangle A1B1C1 is constructed above the height of the equilateral triangle ABC is constructed as. Above the height of the equilateral triangle A1B1C1 is built triangle A2B2C2, and so on. The procedure is repeated continuously. What is the - Series and sequences
 Find a fraction equivalent to the recurring decimal. 0.435643564356
Find a fraction equivalent to the recurring decimal. 0.435643564356
- Miraculous tree
 The miraculous tree grows so fast that the first day increases its height by half the total height of the second day by the third, the third day by a quarter, etc. How many times will it increase its height after 6 days?
The miraculous tree grows so fast that the first day increases its height by half the total height of the second day by the third, the third day by a quarter, etc. How many times will it increase its height after 6 days? - Saving per cents
 The first day I saved 1 cent and every following day a cent more. How many do I save in one year (365 days)?
The first day I saved 1 cent and every following day a cent more. How many do I save in one year (365 days)? - Decimal to fraction
 Write the decimal number 8.638333333 as a fraction A/B in the basic form. Given decimal has infinite repeating figures.
Write the decimal number 8.638333333 as a fraction A/B in the basic form. Given decimal has infinite repeating figures. - Fraction
 Fraction frac(0, overline(38))(0,38) write as fraction a/b, a, b is integers numerator/denominator.
Fraction frac(0, overline(38))(0,38) write as fraction a/b, a, b is integers numerator/denominator. - Ayden
 Ayden is 140 cm tall, and his friend Alex is 1/5 taller than him. How tall is Alex?
Ayden is 140 cm tall, and his friend Alex is 1/5 taller than him. How tall is Alex?
- Offset the mean
 The mean of 16 numbers is 8. If 2 is added to every number, what will be the new mean?
The mean of 16 numbers is 8. If 2 is added to every number, what will be the new mean? - Prawns and carbs
 I buy 3 1/4 kg of prawns and 4 2/5 kg of carbs. 1 kg of prawns is RM 24 and 1 kg of carbs is RM 10. If I pay RM 50, what is my change?
I buy 3 1/4 kg of prawns and 4 2/5 kg of carbs. 1 kg of prawns is RM 24 and 1 kg of carbs is RM 10. If I pay RM 50, what is my change? - Mean and sum
 If the arithmetic mean of 6 numbers is 45, what is the total sum of these numbers?
If the arithmetic mean of 6 numbers is 45, what is the total sum of these numbers? - Tricky result
 Classic adding with percentages: Evaluate 28% of 450 + 45% of 280
Classic adding with percentages: Evaluate 28% of 450 + 45% of 280 - A cake 2
 Karen sliced a cake into 10 slices. She ate 2/10 of it and after some time she ate another 4/10 of it. How much of the cake did Karen eat?
Karen sliced a cake into 10 slices. She ate 2/10 of it and after some time she ate another 4/10 of it. How much of the cake did Karen eat?
- Katy bought
 Katy bought 4/5 kg of oranges, 2 1/2 kg of bananas, and 1 1/2 kg of apples every day. How many kilograms of fruit did she buy each day?
Katy bought 4/5 kg of oranges, 2 1/2 kg of bananas, and 1 1/2 kg of apples every day. How many kilograms of fruit did she buy each day? - Summer vacation
 Rekha spent 3/8 of her summer vacation in Delhi, 1/16 in Mumbai, and ¼ in Chennai. What fraction of her summer vacation did he spend in all?
Rekha spent 3/8 of her summer vacation in Delhi, 1/16 in Mumbai, and ¼ in Chennai. What fraction of her summer vacation did he spend in all? - Lara's sequence
 Lara starts with a number less than 20. She divides it by 2 and adds 6. She then divides this result by 3. Her answer is 4.5. What number does she start with?
Lara starts with a number less than 20. She divides it by 2 and adds 6. She then divides this result by 3. Her answer is 4.5. What number does she start with?
