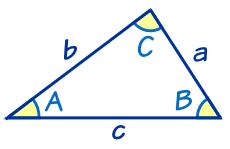
Side c
In △ABC a=1, b=6 and ∠C=110°.
Calculate the length of the side c.
Calculate the length of the side c.
Correct answer:
Tips for related online calculators
Do you want to convert length units?
The Pythagorean theorem is the base for the right triangle calculator.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
The Pythagorean theorem is the base for the right triangle calculator.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
arithmeticplanimetricsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Triangle's centroid
In the triangle ABC the given lengths of its medians tc = 9, ta = 6. Let T be the intersection of the medians (triangle's centroid), and the point S is the center of the side BC. The magnitude of the CTS angle is 60°. Calculate the length of the BC side t - Euclid2
The ABC right triangle with a right angle at C is side a=29 and height v=17. Calculate the perimeter of the triangle. - Sides ratio and angles
In triangle ABC, you know the ratio of side lengths a:b:c=3:4:6. Calculate the angle sizes of triangle ABC. - The right triangle
In the right triangle ABC with a right angle at C, we know the side lengths AC = 9 cm and BC = 7 cm. Calculate the length of the remaining side of the triangle and the size of all angles.
- Triangle ABC
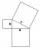Right triangle ABC with right angle at the C, |BC|=19, |AB|=26. Calculate the height of the triangle hAB to the side AB. - Median
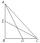In the ABC triangle is given side a=10 cm and median to side a: ta= 13 cm, and angle gamma 90°. Calculate the length of the median to side b (tb). - Cosine
Cosine and sine theorem: Calculate all unknown values (side lengths or angles) from triangle ABC. c = 2.9 cm; β = 28°; γ = 14° α =? °; a =? cm; b =? cm
