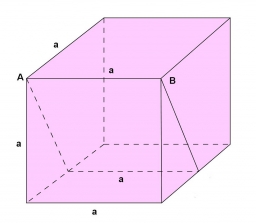
Cube cut
The edge of the CC' guides the ABCDA'B'C'D'cube, a plane that divides the cube into two perpendicular four-sided and triangular prisms, whose volumes are 3:2. Determine which ratio the edge AB divides by this plane.
Final Answer:
Tips for related online calculators
Check out our ratio calculator.
See also our right triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
arithmeticsolid geometryplanimetricsbasic operations and conceptsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Triangular prism
The plane passing through the edge AB and the center of segment CC' of regular triangular prism ABCA'B'C' has an angle with base 30 degrees, |AB| = 15 cm. Calculate the volume of the prism. - 3s prism
A regular perpendicular triangular prism with a height of 19.0 cm and a base edge of 7.1 cm is given. Calculate the prism's volume. - In plane 2
A triangle ABC is located in the plane with a right angle at vertex C, for which the following holds: A(1, 2), B(5, 2), C(x, x+1), where x > -1. a) determine the value of x b) determine the coordinates of point M, which is the midpoint of line segment - A cone 4
A cone with a radius of 10 cm is divided into two parts by drawing a plane through the midpoint of its axis parallel to its base. Compare the volumes of the two parts. - Isosceles weight
A designer weight is made from a glass cube by cutting a three-sided prism with an isosceles triangle base that is right-angled and whose arm is half the length of the cube edge. What percentage of the cube is cut off when making the weight? - The projection
In axonometry, construct the projection of a perpendicular 4-sided pyramid with a square base ABCD in the plane. The base triangle gives the axonometry. We know the center of the base S, the point of the base A, and the height of the pyramid v. - Cube corners
From the cube of edge 24 cm, we cut off all vertices so that each cutting plane intersects the edges 2 cm from the nearest vertice. How many edges will this body have?
