Rez kocky rovinou
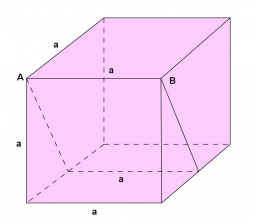
V kocke ABCDA'B'C'D' je vedená hranou CC' rovina tak, že rozdelí kocku na dva kolmé hranoly, štvorboký a trojboký, ktorých objemy sú v pomere 3:2. Určte v akom pomere je touto rovinou rozdelená hrana AB.
Vaša odpoveď:
Vaša odpoveď:
Tipy na súvisiace online kalkulačky
Vyskúšajte našu kalkulačka na prepočet pomeru.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Tip: premeniť jednotky objemu vám pomôže naša kalkulačka premeny jednotiek objemu.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Tip: premeniť jednotky objemu vám pomôže naša kalkulačka premeny jednotiek objemu.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
aritmetikastereometriaplanimetriazákladné operácie a pojmyJednotky fyzikálnych veličínÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Trojboký hranol
Rovina, ktorá prechádza hranou AB a stredom hrany CC´ pravidelného trojbokého hranola ABCA´B´C´, zviera s podstavou uhol 30 stupňov, |AB| = 5 cm. Vypočítajte objem hranola. - Objem 10
Objem kocky a kvadra je v pomere 3:2. Objem gule a kvadra je v pomere 1:3. V akom pomere su objemy kocky, kvadra a gule? - Povrchy v pomere
Objemy dvoch kociek sú v pomere 27:8. V akom pomere sú povrchy týchto kociek? - Kocke
Kocke je vpísaná guľa. Určte jej objem, ak je hrana kocky 10 cm. - Záhada zo stereometrie
Dva pravidelné štvorsteny majú povrchy 72 cm² a 162 cm². V akom pomere sú ich objemy? Zapíšte ako zlomok a ako riešenie zapíšte aj ako desatinné číslo zaokrúhlené na 4 desatinné miesta. - Plastelína Rasťo vymodeloval z plastelíny kváder s rozmermi 2 cm,4 cm,9 cm. Potom plastelínu rozdelil na dve časti v pomere 1:8 z každej časti urobil kocku. V akom pomere sú povrchy týchto kociek?
- 4BH - podstavná hrana
Je daný pravidelný štvorboký hranol ABCDEFGH s podstavnou hranou AB dĺžky 8 cm a výškou 6 cm. Bod M je stred hrany AE. Určte vzdialenosť bodu M od roviny BDH.
