V krychli
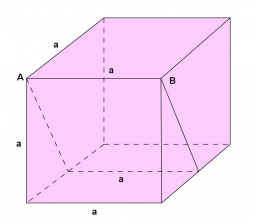
V krychli ABCDA´B´C´D´ je vedena hranou CC´ rovina tak, že rozdělí krychli na dva kolmé hranoly, čtyřboký a trojboký, jejichž objemy jsou v poměru 3 : 2. Určete v jakém poměru je touto rovinou rozdělena hrana AB.
Vaše odpověď:
Vaše odpověď:
Tipy na související online kalkulačky
Vyzkoušejte naši kalkulačka na přepočet poměru.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
aritmetikastereometrieplanimetriezákladní operace a pojmyJednotky fyzikálních veličinÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Krychle
Objemy dvou krychlí jsou v poměru 27:8. V jakém poměru jsou povrchy těchto krychlí? - Trojboký hranol
Rovina, která prochází hranou AB a středem hrany CC' pravidelného trojbokého hranolu ABCA'B'C', svírá s podstavou úhel 46 stupňů, |AB| = 12 cm. Vypočítejte objem hranolu. - Trojitý poměr
Objem kostky a kvádru je v poměru 3:2. Objem koule a kvádru je v poměru 1:3. V jakém poměru jsou objemy kostky, kvádru a koule? - Záhada ze stereometrie
Dva pravidelné čtyřstěny mají povrchy 72 cm² a 162 cm². V jakém poměru jsou jejich objemy? Zapište jako zlomek a jako řešení zapište i jako desetinné číslo zaokrouhleno na 4 desetinná místa. - Rozdělení úsečky
AB usečka =14 cm, rozděl ji na dvě úsečky, jejichž délky jsou v poměru 4:3. - Bonbony
V sáčku jsou bonbony červené, modré a zelené. Červených je k zeleným v poměru 6:11 a modrých k červeným v poměru 7:5. V jakém poměru jsou modré a zelené bonbony? - Těleso 11
Těleso spočívá na nakloněné rovině a působí na ní tlakovou silou o velikosti 70 N. Určete jaký úhel svírá nakloněná rovina s vodorovnou rovinou jestliže na těleso působí tíhová síla o velikosti 100 N.
