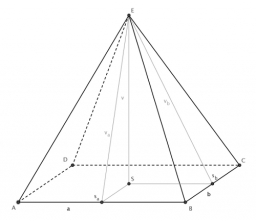
Tetrahedral pyramid
Calculate the surface S and the volume V of a regular tetrahedral pyramid with the base side a = 5 m and a body height of 14 m.
Correct answer:
Tips for related online calculators
See also our right triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
arithmeticsolid geometryplanimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- 216 surface area and volume
Calculate the surface area and volume of a regular tetrahedral pyramid: a = 6 cm and the body height is 12 cm. - Quadrangular pyramid
Given is a regular quadrangular pyramid with a square base. The body height is 30 cm, and volume V = 1000 cm³. Calculate its side and its surface area. - Hypotenuse 78844
Construct triangle KLM if side m=6.5cm, hypotenuse tm=4cm, height to side m: vm=3.2cm - Rotational motion of a cylinder
Calculate the kinetic energy of a cylindrical body of radius r= 0.08 meter and mass m= 1.5kg at time t= 5 s, if this body rotates around an axis passing through the center of the cylinder with a constant acceleration Ԑ= 5 rad/s², if at time t=. - Tetrahedral pyramid
A regular tetrahedral pyramid is given. Base edge length a = 6.5 cm, side edge s = 7.5 cm. Calculate the volume and the area of its face (side area). - Quadrilateral 6353
Given is a regular quadrilateral pyramid with a square figure. Side = 16 cm, S = 736 cm². Calculate h (body height) and body volume V. - Quadrilateral 82052
Calculate the volume of a regular quadrilateral pyramid with a square base of side a=8 cm and a height of the pyramid of 11 cm.
