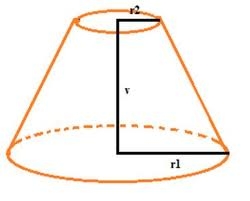
The cone
The cone has a base radius of 12 cm and a height of 20 cm. It was truncated at 6 cm from the base. We created a truncated cone - frustum. Find the radius of the base of the truncated cone.
Correct answer:
Tips for related online calculators
Check out our ratio calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
solid geometryplanimetricsbasic operations and conceptsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Truncated cone
Calculate the volume of a truncated cone with base radiuses r1=19 cm, r2 = 11 cm, and height v = 5 cm. - Lamp cone
Calculate the surface of a lampshade shaped like a rotary truncated cone with a base diameter of 32 cm and 12 cm and a height of 24 cm. - Frustrum - volume, area
Calculate the surface and volume of a truncated rotating cone with base radii of 8 cm and 4 cm and a height of 5 cm. - Truncated cone
A truncated cone has bases with 40 cm and 10 cm radiuses and a height of 25 cm. Calculate its surface area and volume.
- Cylinder-shaped part
A truncated cone-shaped part with base radii of 4 cm and 22 cm is to be recast into a cylinder-shaped part of the same height as the original part. What base radius will the new part have? - Frustrum - volume, area
Calculate the surface and volume of the truncated cone. The radius of the smaller figure is 4 cm, the height of the cone is 4 cm, and the side of the truncated cone is 5 cm. - Truncated cone 5 The height of a cone is 7 cm, the length of a side is 10 cm, and the lower radius is 3cm. What could be the possible answer for the upper radius of a truncated cone?
