Kužeľ 19
Kužeľ s polomerom podstavy 12 cm a výškou 20 cm bol vo vzdialenosti 6 cm od podstavy zrezaný, čím vznikol zrezaný kužeľ. Zistite polomer podstavy zrezaného kužeľa.
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Vyskúšajte našu kalkulačka na prepočet pomeru.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
stereometriaplanimetriazákladné operácie a pojmyÚroveň náročnosti úlohy
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
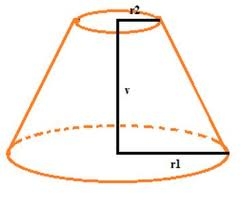
- Zrezaný kúžeľ
Vypočítajte objem zrezaného kúžeľa s polomermi podstáv r1=18 cm, r2 = 6 cm a výškou v = 17 cm. - Zrezaný kužeľ 8
Vypočítaj povrch a objem zrezaného rotačného kužeľa s polomermi podstáv 8 cm a 4 cm, výškou 5 cm. - Rotačný kúžeľ
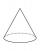Vypočítajte objem rotačného kužeľa s polomerom podstavy r=10 cm a výškou v=10 cm. - Objem kužeľa
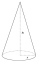Vypočítajte objem kužeľa s polomerom podstavy r a výškou v. a) r = 6 cm, v = 8 cm b) r = 0,9 m, v = 2,3 m c) r = 1,4 dm, v = 30 dm - Lampa - tienidlo
Vypočítajte povrch lampového tienidla v tvare rotačného zrezaného kužeľa s priemermi podstáv 32 cm a 12 cm a výškou 24 cm. - Vypočítajte 45
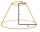Vypočítajte povrch a objem zrezaného rotačného kužeľa s polomermi podstáv 14cm a 8cm, výškou 11cm. - Zrezaný 13
Zrezaný rotačný kužeľ má podstavy s polomermi r1 = 8 cm, r2 = 4 cm a výšku v = 5 cm. Aký je objem kužeľa, z ktorého zrezaný kužeľ vznikol?
