Ratio of volumes
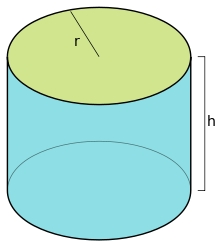
If the heights of two cylindrical drums are in the ratio 7:8 and their base radii are in the ratio 4:3. What is the ratio of their volumes?
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
algebrasolid geometryplanimetricsbasic operations and conceptsUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Right circular cone
The volume of a right circular cone is 5 liters. The cone is divided by a plane parallel to the base, one-third down from the vertex to the base. Calculate the volume of these two parts of the cone. - Mystery of stereometrie
Two regular tetrahedrons have surfaces 92 cm² and 207 cm². In what ratio are their volumes? Write as a fraction and as a decimal rounded to 4 decimal places. - Three ratios 2
What is the ratio of bases of two triangles when the ratio of their heights is 3:4 and the ratio of their areas is 4:3? - Spheres - ratios
The surface area of two spheres are in the ratio 1 : 4 . Find the ratio of their volumes.
- Surfaces 3793
The volumes of the two cubes are in the ratio of 27:8. What is the ratio of the surfaces of these cubes? - Ratio
The radii of the two cones are in the ratio of 5.7. Calculate the area ratio of cones that have the same height. - Perpendicular 82488
For the volumes of a perpendicular prism and a pyramid with the same base and height: A) the volumes are equal B) the volume of a pyramid is three times smaller than the volume of a prism C) the ratio of the volumes of the prism and the pyramid is 1:3 D)
