Base of prism
The base of the perpendicular prism is a rectangular triangle whose legs lengths are at a 3:4 ratio. The height of the prism is 2cm smaller than the larger base leg. Determine the volume of the prism if its surface is 468 cm2.
Correct answer:

Tips for related online calculators
See also our right triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- solid geometry
- surface area
- prism
- planimetrics
- Pythagorean theorem
- right triangle
- area of a shape
- triangle
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Perimeter 83259
 The perimeter of the four-sided needle is 48 m, and its height is 2.5 m; how much will the sheet metal for this pyramid cost? If 1m² costs €1.5, a 12% loss due to joints and folds is included in the area.
The perimeter of the four-sided needle is 48 m, and its height is 2.5 m; how much will the sheet metal for this pyramid cost? If 1m² costs €1.5, a 12% loss due to joints and folds is included in the area. - A frustum
 A frustum of a pyramid consists of a square base of length 10 cm and a top square of length 7 cm. The height of the frustum is 6 cm. Calculate the surface area and volume.
A frustum of a pyramid consists of a square base of length 10 cm and a top square of length 7 cm. The height of the frustum is 6 cm. Calculate the surface area and volume. - Tent - spherical cap
 I have a tent in the shape of a spherical cap. Assume we want the volume to be 4 cubic meters, to sleep two or three people. Assume that the material making up the dome of the ten is twice as expensive per square as the material touching the ground. What
I have a tent in the shape of a spherical cap. Assume we want the volume to be 4 cubic meters, to sleep two or three people. Assume that the material making up the dome of the ten is twice as expensive per square as the material touching the ground. What - Januka
 Januka and her father were going to the tent. They found that their old tent was torn. Their mother suggested that they sew a tent whose walls would be made of 4 identical isosceles triangles. Their lower side is 2 m long, and the height is also 2 m. Then
Januka and her father were going to the tent. They found that their old tent was torn. Their mother suggested that they sew a tent whose walls would be made of 4 identical isosceles triangles. Their lower side is 2 m long, and the height is also 2 m. Then
- A lamp
 A lamp shade like that of a frustum has a height of 12 cm and an upper and lower diameter of 10 cm and 20 cm. What area of materials is required to cover the curved surface of the frustum?
A lamp shade like that of a frustum has a height of 12 cm and an upper and lower diameter of 10 cm and 20 cm. What area of materials is required to cover the curved surface of the frustum? - Saria
 Saria is wrapping a gift for her mother. The gift box is in the shape of a rectangular prism and is 5 centimeters high, 25 centimeters long, and 40 centimeters wide. How much wrapping paper will you need to wrap the gift box?
Saria is wrapping a gift for her mother. The gift box is in the shape of a rectangular prism and is 5 centimeters high, 25 centimeters long, and 40 centimeters wide. How much wrapping paper will you need to wrap the gift box? - Cross-section 81879
 The castle has a length of 4 m and a cross-section in the shape of a square whose side is 15 cm long. Eight such castles must be painted. One kilogram can is enough for 6 m² of coating. How many cans of paint should be bought?
The castle has a length of 4 m and a cross-section in the shape of a square whose side is 15 cm long. Eight such castles must be painted. One kilogram can is enough for 6 m² of coating. How many cans of paint should be bought? - A bakery
 A bakery makes cylindrical mini muffins that measure 2 inches in diameter and one and one-fourth inches in height. If each mini muffin is completely wrapped in paper, then at least how much paper is needed to wrap 6 mini muffins? Approximate using pi equa
A bakery makes cylindrical mini muffins that measure 2 inches in diameter and one and one-fourth inches in height. If each mini muffin is completely wrapped in paper, then at least how much paper is needed to wrap 6 mini muffins? Approximate using pi equa - Calculate 397
 Calculate the surface of a spire with a base in the shape of a rectangle with dimensions of 5m and 6m. The height of the spire is 7m.
Calculate the surface of a spire with a base in the shape of a rectangle with dimensions of 5m and 6m. The height of the spire is 7m.
- Centimeters 81623
 The warehouse has the shape of a cuboid with dimensions: length of 50 meters, width of 600 decimeters, and height of 300 centimeters. Calculate how much it will cost to paint a windowless room with a door 150 centimeters wide and 200 centimeters high (the
The warehouse has the shape of a cuboid with dimensions: length of 50 meters, width of 600 decimeters, and height of 300 centimeters. Calculate how much it will cost to paint a windowless room with a door 150 centimeters wide and 200 centimeters high (the - Create 6
 Create a new drink can that will double the volume of the original can used. Dimensions of the can: 6cm diameter and 10cm height. You are to double the volume with the least amount of additional aluminum needed for the new can. There are 3 options : Optio
Create a new drink can that will double the volume of the original can used. Dimensions of the can: 6cm diameter and 10cm height. You are to double the volume with the least amount of additional aluminum needed for the new can. There are 3 options : Optio - Storage shed
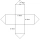 Frank designed a net for a storage shed that he is going to construct out of metal. The design consists of a square base and four square sides, plus four triangular parts that make up the roof. A square base of 6 feet and four square sides, plus 4 feet of
Frank designed a net for a storage shed that he is going to construct out of metal. The design consists of a square base and four square sides, plus four triangular parts that make up the roof. A square base of 6 feet and four square sides, plus 4 feet of - A cone 3
 A cone has a diameter of x cm and a slant height of y cm. A square pyramid has a base side length of x cm and a slant height of y cm. Which has the greater surface area? Explain.
A cone has a diameter of x cm and a slant height of y cm. A square pyramid has a base side length of x cm and a slant height of y cm. Which has the greater surface area? Explain. - The perimeter
 The perimeter of the base of a regular quadrilateral pyramid is the same as its height. The pyramid has a volume of 288 dm³. Calculate its surface area round the result to the whole dm².
The perimeter of the base of a regular quadrilateral pyramid is the same as its height. The pyramid has a volume of 288 dm³. Calculate its surface area round the result to the whole dm².
- The area 4
 The area of a 2 dm high cylinder with a diameter of 1 dm equals how much dm²?
The area of a 2 dm high cylinder with a diameter of 1 dm equals how much dm²? - A piece 7
 A piece of dry ice is in the shape of a cube with edge lengths of 7cm. Find the surface area of the dry ice.
A piece of dry ice is in the shape of a cube with edge lengths of 7cm. Find the surface area of the dry ice. - Classroom 80652
 The classroom is 11 m long, 6.5 m wide, and 4 m high. I will pay 14.50 for 1 m² of painting. How much will it cost to paint the classroom?
The classroom is 11 m long, 6.5 m wide, and 4 m high. I will pay 14.50 for 1 m² of painting. How much will it cost to paint the classroom?
