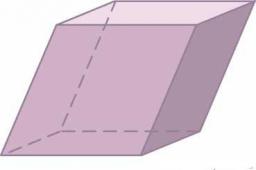
Prism
Calculate the volume of the rhombic prism. The prism base is a rhombus whose one diagonal is 47 cm, and the edge of the base is 27 cm. The edge length and height of the base of the prism are 4:3.
Correct answer:
Tips for related online calculators
Do you want to convert length units?
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
arithmeticsolid geometryplanimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Quadrilateral 23881
Calculate the height of a regular quadrilateral prism whose base is a rhombus. The edge in the base is 7 cm long, the opposite edges are 5 cm apart, and we also know that the entire body has a volume of 1dm³. - Rhombus base
Calculate the volume and surface area of prisms whose base is a rhombus with diagonals u1 = 12 cm and u2 = 15 cm. The prism height is twice the base edge length. - Calculate diagonals
Calculate the length of the solid diagonals of a prism with a rhombus base if the sizes of the base diagonals are 16 cm and 20 cm and the height of the prism is 32 cm. Calculate the size of the base edge. - Calculate 23411
The prism with a diamond base has one base diagonal of 20 cm and a base edge of 26 cm. The edge of the base is 2:3 to the height of the prism. Calculate the volume of the prism. - Triangular 80766
Calculate the volume of a regular triangular prism whose height is equal to the length of the base edge. Calculate the volume for the edge length a = 6 cm. - Support colum
Calculate the support column's volume and surface. It is shaped as a vertical quadrangular prism whose base is a rhombus with diagonals u1 = 102 cm and u2 = 64 cm. The column height is 1. 5m. - Corresponding 67714
The quadrilateral prism has a volume of 720 cm³. Calculate the height of the prism if the base is a rhombus with a side 16 cm long and a corresponding height of 5 cm.
