Pythagorean theorem - practice problems - page 4 of 73
Number of problems found: 1449
- Calculate
 Calculate the length of a side of the equilateral triangle with an area of 50cm².
Calculate the length of a side of the equilateral triangle with an area of 50cm². - Isosceles triangle
 Calculate the area of an isosceles triangle, the base measuring 16 cm and the arms 10 cm.
Calculate the area of an isosceles triangle, the base measuring 16 cm and the arms 10 cm. - Leg and height
 Solve right triangle with height v = 7.8 m and shorter cathetus b = 15 m.
Solve right triangle with height v = 7.8 m and shorter cathetus b = 15 m. - ABS CN
 Calculate the absolute value of the complex number -6+19i.
Calculate the absolute value of the complex number -6+19i. - The diagonal 4
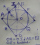 The diagonal of a rhombus measures 16 cm and 30 cm. Find its perimeter.
The diagonal of a rhombus measures 16 cm and 30 cm. Find its perimeter. - One leg
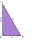 One leg of a right triangle is 1 foot longer than the other leg. The hypotenuse is 5 feet. Find the lengths of the three sides of the triangle.
One leg of a right triangle is 1 foot longer than the other leg. The hypotenuse is 5 feet. Find the lengths of the three sides of the triangle. - Equilateral Δ
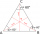 What is the area of an equilateral triangle with a circumference of 63 cm?
What is the area of an equilateral triangle with a circumference of 63 cm? - Annular area
 The square with side a = 1 is inscribed and circumscribed by circles. Find the annular area.
The square with side a = 1 is inscribed and circumscribed by circles. Find the annular area. - Find radius
 Find the radius of the circle using the Pythagorean theorem where a=9, b=r, c= 6+r
Find the radius of the circle using the Pythagorean theorem where a=9, b=r, c= 6+r - Diagonal of square
 Calculate the side of a square when its diagonal is 10 cm.
Calculate the side of a square when its diagonal is 10 cm. - Catheti
 The hypotenuse of a right triangle is 35, and the sum of legs is 49. Calculate the length of its legs.
The hypotenuse of a right triangle is 35, and the sum of legs is 49. Calculate the length of its legs. - Isosceles IV
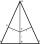 In an isosceles triangle ABC is |AC| = |BC| = 13 and |AB| = 10. Calculate the radius of the inscribed (r) and described (R) circle.
In an isosceles triangle ABC is |AC| = |BC| = 13 and |AB| = 10. Calculate the radius of the inscribed (r) and described (R) circle. - Triangle 36091
 Decide if the triangle is right (sides 5,11,7, cm)
Decide if the triangle is right (sides 5,11,7, cm) - Equilateral triangle v3
 Calculate an equilateral triangle's perimeter and area with a side of 20 dm.
Calculate an equilateral triangle's perimeter and area with a side of 20 dm. - Tv screen
 The length of its diagonal gives the size of a tv screen. If the dimension of a tv screen is 16 inches by 14 inches, what is the TV screen size?
The length of its diagonal gives the size of a tv screen. If the dimension of a tv screen is 16 inches by 14 inches, what is the TV screen size? - Is right triangle
 Decide if the triangle XYZ is rectangular: x = 4 m, y = 6 m, z = 4 m
Decide if the triangle XYZ is rectangular: x = 4 m, y = 6 m, z = 4 m - Calculate hypotenuse
 Calculate the hypotenuse of a right triangle PT if the length of one hypotenuse is 1.2 dm and the length of the hypotenuse is 1.3 dm.
Calculate the hypotenuse of a right triangle PT if the length of one hypotenuse is 1.2 dm and the length of the hypotenuse is 1.3 dm. - Diamond
 Calculate the length of the two diagonals of the diamond if: a = 13 cm v = 12 cm
Calculate the length of the two diagonals of the diamond if: a = 13 cm v = 12 cm - Circles
 The area of a circle inscribed in a square is 7. What is the area of a circle circumscribed around a square?
The area of a circle inscribed in a square is 7. What is the area of a circle circumscribed around a square? - Median
 In the right triangle are sides a=96 dm b=31 dm. Calculate the length of the medians tc to the hypotenuse.
In the right triangle are sides a=96 dm b=31 dm. Calculate the length of the medians tc to the hypotenuse.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
