Angle - math word problems - page 22 of 64
Number of problems found: 1264
- Triangle angle ratio
The sizes of the interior angles of the triangle are in a successive ratio of 6:4:5 are these angles big? - Tower's view
From the church tower's view at 65 m, the top of the house can be seen at a depth angle of alpha = 45° and its bottom at a depth angle of beta = 58°. Calculate the house's height and its distance from the church. - Aircraft
From the aircraft flying at an altitude of 500m, they observed places A and B (at the same altitude) in the direction of flight at depth angles alpha = 48° and beta = 35°. What is the distance between places A and B? - The roof
The tower's roof has the shape of a regular quadrangular pyramid, the base edge of which is 11 m long, and the side wall of the animal with the base at an angle of 57°. Calculate how much roofing we need to cover the entire roof if we count on 15% waste. - Altitude angle
In complete winds-free weather, the balloon took off and remained standing exactly above the place from which it took off. It is 250 meters away from us. How high did the balloon fly when we saw it at an altitude angle of 25°? - Tower distance
From the lookout tower, 70 meters high, we see a man at a depth angle of 15 degrees. Calculate how far one stands from the base of the lookout tower. Draw and calculate. - Angle of inclination
What percentage of the gradient should be indicated on the mark if the angle of inclination of the road is 6°25'? - Triangle's centroid
In the triangle ABC the given lengths of its medians tc = 9, ta = 6. Let T be the intersection of the medians (triangle's centroid), and the point S is the center of the side BC. The magnitude of the CTS angle is 60°. Calculate the length of the BC side t - Temperature drops
If the temperature of a city drops 2° every day and increases by 3° every five days, how long does it take to drop to -15° from temperature +5°? - Altitude angles Cities A, B, and C lie in one elevation plane. C is 50 km east of B, and B is north of A. C is deviated by 50° from A. The plane flies around places A, B, and C at the same altitude. When the aircraft is flying around B, its altitude angle to A is 12°. Fi
- Base diagonal
In a regular four-sided pyramid, the side edge forms an angle of 55° with the base's diagonal. The length of the side edge is eight meters. Calculate the pyramid's surface area and volume. - Side edges
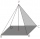The regular 4-sided pyramid has a body height of 2 dm, and the opposite side edges form an angle of 70°. Calculate the surface area and volume of the pyramid. - Diagonals of a prism
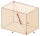The base of the square prism is a rectangle with dimensions of 3 dm and 4 dm. The height of the prism is 1 m. Find out the angle between the body diagonal and the base's diagonal. - Aircraft bearing Two aircraft will depart from the airport simultaneously. The first flight flies with a course of 30°, and the second with a course of 86°. Both fly at 330 km/h. How far apart will they be in 45 minutes of flight?
- MO Z7–I–6 2021
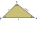In triangle ABC, point D lies on the AC side and point E on the BC side. The sizes of the angles ABD, BAE, CAE, and CBD are 30°, 60°, 20°, and 30°, respectively. Find the size of the AED angle. - Geometry exercise
Calculations from geometry: The ratios of the sides of the quadrilateral are 3 : 6:4.5 : 3.5. Calculate their lengths if the circumference is 51 cm. The sizes of the angles in the quadrilateral are equal to 29°30', 133°10', and 165°20'. What is the size o - Modulus and argument
Find the mod z and argument z if z=i - The body
The body slides down an inclined plane, forming an angle α = π / 4 = 45° under the action of a horizontal plane under the effect of friction forces with acceleration a = 2.4 m/s². At what angle β must the plane be inclined so that the body slides on it af - Tangens parallelogram
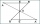
If ∠BAD between the sides AB and AD of the parallelogram is θ, what is tan θ? See diagram: A=(7,1) B=(5,-2) C=(12,1) D=(14,4) - Second hand path
What path will the end of the second hand make in 24 minutes if it is 5 cm long?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
