Practice problems of the area of a quadrilateral
Number of problems found: 82
- Square
 Square JKLM has sides of a length of 24 cm. Point S is the center of LM. Calculate the area of the quadrant JKSM in cm².
Square JKLM has sides of a length of 24 cm. Point S is the center of LM. Calculate the area of the quadrant JKSM in cm². - Quadrilateral
 In the square ABCD point, P is in the middle of the DC side, and point Q is in the middle of side AD. If the area of quadrilateral BQPC is 76 cm², what is the area of ABCD?
In the square ABCD point, P is in the middle of the DC side, and point Q is in the middle of side AD. If the area of quadrilateral BQPC is 76 cm², what is the area of ABCD? - The quadrilateral
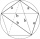 The quadrilateral ABCD is composed of two right triangles, ABD and BCD. For side lengths: |AD| = 3cm, | BC | = 12cm, | BD | = 5cm. How many square centimeters (area) does the quadrilateral ABCD have? The angles of DAB and DBC are right.
The quadrilateral ABCD is composed of two right triangles, ABD and BCD. For side lengths: |AD| = 3cm, | BC | = 12cm, | BD | = 5cm. How many square centimeters (area) does the quadrilateral ABCD have? The angles of DAB and DBC are right. - Parallelogram ABCD
 The area of parallelogram ABCD is 902 cm². Points M and N are the midpoints of the sides AB and BC. What is the area of a quadrilateral MBND?
The area of parallelogram ABCD is 902 cm². Points M and N are the midpoints of the sides AB and BC. What is the area of a quadrilateral MBND?
- Quadrilateral 66614
 The picture shows a square ABCD with the center S and the side 8 cm long. Point E is any point on the CD side other than C and D. Calculate the area of the ASBE quadrilateral in cm².
The picture shows a square ABCD with the center S and the side 8 cm long. Point E is any point on the CD side other than C and D. Calculate the area of the ASBE quadrilateral in cm². - Perpendicular 81381
 Which parking lot for 5 cars occupies a larger area, perpendicular or inclined at an angle of 45°, and how much? the car has dimensions of 4m and 2m.
Which parking lot for 5 cars occupies a larger area, perpendicular or inclined at an angle of 45°, and how much? the car has dimensions of 4m and 2m. - Quadrilateral calc
 The square ABCD is given. The midpoint of AB is E, the midpoint of BC is F, CD is G, and the midpoint of DA is H. Join AF, BG, CH, and DE. Inside the square (approximately in the middle), the intersections of these line segments form a quadrilateral. Calc
The square ABCD is given. The midpoint of AB is E, the midpoint of BC is F, CD is G, and the midpoint of DA is H. Join AF, BG, CH, and DE. Inside the square (approximately in the middle), the intersections of these line segments form a quadrilateral. Calc - Parallelogram ABCD
 We have the parallelogram ABCD, where AB is 6.2 cm BC is 5.4 cm AC is 4.8 cm calculate the height on the AB side and the angle DAB
We have the parallelogram ABCD, where AB is 6.2 cm BC is 5.4 cm AC is 4.8 cm calculate the height on the AB side and the angle DAB - Quadrilateral 23881
 Calculate the height of a regular quadrilateral prism whose base is a rhombus. The edge in the base is 7 cm long, the opposite edges are 5 cm apart, and we also know that the entire body has a volume of 1dm³.
Calculate the height of a regular quadrilateral prism whose base is a rhombus. The edge in the base is 7 cm long, the opposite edges are 5 cm apart, and we also know that the entire body has a volume of 1dm³.
- Quadrilateral-trapezoid 3172
 We cut two triangles from the rectangular plate so that the resulting quadrilateral-trapezoid with the same arm lengths has an area of 32 cm², and one of its bases is twice as long as the other. What is the area of the two triangles that make up the waste
We cut two triangles from the rectangular plate so that the resulting quadrilateral-trapezoid with the same arm lengths has an area of 32 cm², and one of its bases is twice as long as the other. What is the area of the two triangles that make up the waste - Rectangular 61183
 Mr. Nový exchanged his rectangular plot of 5.2 hectares with his neighbor for two. The first plot has the shape of a square with a side of 70 m, and the second has the shape of a rectangle with dimensions of 110 m and 410 m. After the exchange, does the n
Mr. Nový exchanged his rectangular plot of 5.2 hectares with his neighbor for two. The first plot has the shape of a square with a side of 70 m, and the second has the shape of a rectangle with dimensions of 110 m and 410 m. After the exchange, does the n - Perpendicular 7223
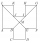 In the ABCDEFGHIJKL, the two adjacent sides are perpendicular to each other, and all sides except the AL and GF sides are identical. The AL and GF parties are twice as long as the other parties. The lines BG and EL intersect at point M. The quadrilateral
In the ABCDEFGHIJKL, the two adjacent sides are perpendicular to each other, and all sides except the AL and GF sides are identical. The AL and GF parties are twice as long as the other parties. The lines BG and EL intersect at point M. The quadrilateral - Quadrilaterals 7224
 In the ABCDEFGHIJKL, the two adjacent sides are perpendicular to each other, and all sides except the AL and GF sides are identical. The AL and GF parties are twice as long as the other parties. The lines BG and EL intersect at point M and divide the dode
In the ABCDEFGHIJKL, the two adjacent sides are perpendicular to each other, and all sides except the AL and GF sides are identical. The AL and GF parties are twice as long as the other parties. The lines BG and EL intersect at point M and divide the dode - Katy MO
 Kate drew a triangle ABC. The middle of the line segment AB has marked as X and the center of the side AC as Y. On the side BC, she wants to find point Z so that the area of a 4gon AXZY is the greatest. What part of the ABC triangle can maximally occupy 4
Kate drew a triangle ABC. The middle of the line segment AB has marked as X and the center of the side AC as Y. On the side BC, she wants to find point Z so that the area of a 4gon AXZY is the greatest. What part of the ABC triangle can maximally occupy 4
- Quadrilateral 82616
 Triangle ABC is divided into line segments. Lines DE and AB are parallel. Triangles CDH, CHI, CIE, and FIH have the same area, namely 8 dm². Find the content of quadrilateral AFHD.
Triangle ABC is divided into line segments. Lines DE and AB are parallel. Triangles CDH, CHI, CIE, and FIH have the same area, namely 8 dm². Find the content of quadrilateral AFHD. - Quadrilateral PQRS
 PQRS is a quadrilateral with P(4,4), S(8,8), and R(12,8). If vector PQ=4*vector SR, find the coordinates of Q. Solve it
PQRS is a quadrilateral with P(4,4), S(8,8), and R(12,8). If vector PQ=4*vector SR, find the coordinates of Q. Solve it - Quadrilateral 58663
 They melted the steel part in the shape of a truncated quadrilateral needle and produced three identical cubes. Determine the surface area of one cube if the edges of the bases of the pyramid are 30 mm and 80 mm and the pyramid's height is 60 mm. I don't
They melted the steel part in the shape of a truncated quadrilateral needle and produced three identical cubes. Determine the surface area of one cube if the edges of the bases of the pyramid are 30 mm and 80 mm and the pyramid's height is 60 mm. I don't - The tent
 The tent shape of a regular quadrilateral pyramid has a base edge length a = 2 m and a height v = 1.8 m. How many m² of cloth did we need to make the tent if we have to add 7% of the seams? How many m³ of air will be in the tent?
The tent shape of a regular quadrilateral pyramid has a base edge length a = 2 m and a height v = 1.8 m. How many m² of cloth did we need to make the tent if we have to add 7% of the seams? How many m³ of air will be in the tent? - Quadrilateral 22003
 The shelter has the shape of a regular quadrilateral pyramid without a front wall. The length of the base edge is 3 meters, and the shelter's height is 3.5 meters. How much canvas must be bought to sew it if we have to increase consumption by 20% for fold
The shelter has the shape of a regular quadrilateral pyramid without a front wall. The length of the base edge is 3 meters, and the shelter's height is 3.5 meters. How much canvas must be bought to sew it if we have to increase consumption by 20% for fold
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
Examples of area of plane shapes. Quadrilateral practice problems.
