Area of Angle Problems - page 10 of 14
Number of problems found: 262
- Isosceles 7566
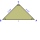 A right isosceles triangle is inscribed in the circle with r = 8 cm. Find triangle area S. How much percent does the triangle occupy the area of the circle?
A right isosceles triangle is inscribed in the circle with r = 8 cm. Find triangle area S. How much percent does the triangle occupy the area of the circle? - Circular segment
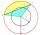 Calculate the area S of the circular segment and the length of the circular arc l. The height of the circular segment is 2 cm, and the angle α = 60°. Help formula: S = 1/2 r². (Β-sinβ)
Calculate the area S of the circular segment and the length of the circular arc l. The height of the circular segment is 2 cm, and the angle α = 60°. Help formula: S = 1/2 r². (Β-sinβ) - Circle 7794
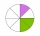 Draw a circle k, r = 4cm, and divide it into two parts in a ratio of 1:5.
Draw a circle k, r = 4cm, and divide it into two parts in a ratio of 1:5. - Hexagon - MO
 The picture shows the ABCD square, the EFGD square, and the HIJD rectangle. Points J and G lie on the side CD and are true |DJ|
The picture shows the ABCD square, the EFGD square, and the HIJD rectangle. Points J and G lie on the side CD and are true |DJ| - Rhombus
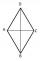 ABCD is a rhombus, ABD is an equilateral triangle, and AC is equal to 4. Find the area of the rhombus.
ABCD is a rhombus, ABD is an equilateral triangle, and AC is equal to 4. Find the area of the rhombus. - Parallelogram - area
 OPRS parallelogram with OP side 4 cm long, OS side 5 cm long, angle at the top P is 100°. What is its area?
OPRS parallelogram with OP side 4 cm long, OS side 5 cm long, angle at the top P is 100°. What is its area? - Four sides of trapezoid
 The trapezoid is given by the length of four sides: 40.5, 42.5, 52.8 35.0. Calculate its area.
The trapezoid is given by the length of four sides: 40.5, 42.5, 52.8 35.0. Calculate its area. - Top of the tower
 The top of the tower has the shape of a regular hexagonal pyramid. The base edge has a length of 1.2 m. The pyramid height is 1.6 m. How many square meters of sheet metal are needed to cover the top of the tower if 15% extra sheet metal is needed for join
The top of the tower has the shape of a regular hexagonal pyramid. The base edge has a length of 1.2 m. The pyramid height is 1.6 m. How many square meters of sheet metal are needed to cover the top of the tower if 15% extra sheet metal is needed for join - Heptagonal pyramid
 A hardwood for a column is in the form of a frustum of a regular heptagonal pyramid. The lower base edge is 18 cm, and the upper base is 14 cm. The altitude is 30 cm. Determine the weight in kg if the wood density is 10 grams/cm³.
A hardwood for a column is in the form of a frustum of a regular heptagonal pyramid. The lower base edge is 18 cm, and the upper base is 14 cm. The altitude is 30 cm. Determine the weight in kg if the wood density is 10 grams/cm³. - The roof
 The tower's roof has the shape of a regular quadrangular pyramid, the base edge of which is 11 m long, and the side wall of the animal with the base at an angle of 57°. Calculate how much roofing we need to cover the entire roof if we count on 15% waste.
The tower's roof has the shape of a regular quadrangular pyramid, the base edge of which is 11 m long, and the side wall of the animal with the base at an angle of 57°. Calculate how much roofing we need to cover the entire roof if we count on 15% waste. - Children pool
 The bottom of the children's pool is a regular hexagon with a = 60 cm side. The distance between opposing sides is 104 cm, and the height of the pool is 45 cm. A) How many liters of water can fit into the pool? B) The pool is made of a double layer of pla
The bottom of the children's pool is a regular hexagon with a = 60 cm side. The distance between opposing sides is 104 cm, and the height of the pool is 45 cm. A) How many liters of water can fit into the pool? B) The pool is made of a double layer of pla - Quadrilateral oblique prism
 What is the volume of a quadrilateral oblique prism with base edges of length a = 1m, b = 1.1m, c = 1.2m, d = 0.7m if a side edge of length h = 3.9m has a deviation from the base of 20° 35' and the edges a, b form an angle of 50.5°?
What is the volume of a quadrilateral oblique prism with base edges of length a = 1m, b = 1.1m, c = 1.2m, d = 0.7m if a side edge of length h = 3.9m has a deviation from the base of 20° 35' and the edges a, b form an angle of 50.5°? - Base RR odd
 The base of the prism is an isosceles trapezoid ABCD with bases AB = 12 cm, and CD = 9 cm. The angle at vertex B is 48° 10'. Determine the volume and area of the prism if its height is 35 cm.
The base of the prism is an isosceles trapezoid ABCD with bases AB = 12 cm, and CD = 9 cm. The angle at vertex B is 48° 10'. Determine the volume and area of the prism if its height is 35 cm. - Paper box
 Calculate the paper consumption on the box-shaped quadrangular prism with rhombic footstall, base edge a=6 cm, and the adjacent base edges form an angle alpha = 60 °. The box height is 10 cm. How much m² of the paper is consumed 100 such boxes?
Calculate the paper consumption on the box-shaped quadrangular prism with rhombic footstall, base edge a=6 cm, and the adjacent base edges form an angle alpha = 60 °. The box height is 10 cm. How much m² of the paper is consumed 100 such boxes? - Approximately 6576
 The honeycomb comprises cells with the shape of a regular 6-sided prism with a base edge length of 3 mm and a corresponding height of 2.6 mm. The height of the prism is 12 mm. How many liters of honey are there in the entire comb if the plastic comprises
The honeycomb comprises cells with the shape of a regular 6-sided prism with a base edge length of 3 mm and a corresponding height of 2.6 mm. The height of the prism is 12 mm. How many liters of honey are there in the entire comb if the plastic comprises - Big Earth
 What percentage of the Earth's surface is seen by an astronaut from a height of h = 350 km? Take the Earth as a sphere with a radius R = 6370 km.
What percentage of the Earth's surface is seen by an astronaut from a height of h = 350 km? Take the Earth as a sphere with a radius R = 6370 km. - Circular pool
 The pool's base is a circle with a radius r = 10 m, excluding a circular segment that determines the chord length of 10 meters. The pool depth is h = 2m. How many hectoliters of water can fit into the pool?
The pool's base is a circle with a radius r = 10 m, excluding a circular segment that determines the chord length of 10 meters. The pool depth is h = 2m. How many hectoliters of water can fit into the pool? - Sphere in cone
 A sphere is inscribed in the cone (the intersection of their boundaries consists of a circle and one point). The ratio of the ball's surface and the area of the base is 4:3. A plane passing through the axis of a cone cuts the cone in an isosceles triangle
A sphere is inscribed in the cone (the intersection of their boundaries consists of a circle and one point). The ratio of the ball's surface and the area of the base is 4:3. A plane passing through the axis of a cone cuts the cone in an isosceles triangle - House roof
 The house's roof is a regular quadrangular pyramid with a base edge 20 m. If the roof pitch is 38° and we calculate 12% of waste, connections, and overlapping of the area roof, how much m² is needed to cover the roof?
The house's roof is a regular quadrangular pyramid with a base edge 20 m. If the roof pitch is 38° and we calculate 12% of waste, connections, and overlapping of the area roof, how much m² is needed to cover the roof? - Cross-section of a roof
 The owner must cover the carport with a hipped roof with a rectangular cross-section of 8 m x 5 m. All roof surfaces have the same slope of 30°. Determine the price and weight of the roof if 1 m² cost €270 and weighs 43 kg.
The owner must cover the carport with a hipped roof with a rectangular cross-section of 8 m x 5 m. All roof surfaces have the same slope of 30°. Determine the price and weight of the roof if 1 m² cost €270 and weighs 43 kg.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
