Basic operations and concepts - math word problems - page 306 of 322
Number of problems found: 6435
- Calculate 4842
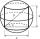 The area of the rotating cylinder shell is half the area of its surface. Calculate the surface of the cylinder if you know that the diagonal of the axial section is 5 cm.
The area of the rotating cylinder shell is half the area of its surface. Calculate the surface of the cylinder if you know that the diagonal of the axial section is 5 cm. - Cube in sphere
 The cube is inscribed in a sphere with a radius r = 6 cm. What percentage is the cube's volume from the ball's volume?
The cube is inscribed in a sphere with a radius r = 6 cm. What percentage is the cube's volume from the ball's volume? - Arithmetic 20153
 The teacher has 12 examples from geometry and 15 examples from arithmetic. How many papers can he create if he wants three examples from geometry and five from arithmetic in the letter?
The teacher has 12 examples from geometry and 15 examples from arithmetic. How many papers can he create if he wants three examples from geometry and five from arithmetic in the letter? - Measuring 6357
 Determine the length of the edge of the cube, the surface of which is equal to 60% of the surface of a block measuring 7cm, 8cm, 6cm
Determine the length of the edge of the cube, the surface of which is equal to 60% of the surface of a block measuring 7cm, 8cm, 6cm - Similarity
 Rectangle ABCD has dimensions of 7 cm and 8 cm. Rectangle PQRS has dimensions 7 cm and 6 cm. Determine the coefficient of the similarity k of the rectangles; if they aren't similar, enter zero as the coefficient of similarity.
Rectangle ABCD has dimensions of 7 cm and 8 cm. Rectangle PQRS has dimensions 7 cm and 6 cm. Determine the coefficient of the similarity k of the rectangles; if they aren't similar, enter zero as the coefficient of similarity. - Logs
 The trunk diameter is 52 cm. Is it possible to inscribe a square prism with a side 27 cm?
The trunk diameter is 52 cm. Is it possible to inscribe a square prism with a side 27 cm? - Ratio 52
 The ratio of the surface area of a cube to its volume is 2:1.Calculate: a) the length of the edge of the cube in cm b) the volume of the cube in cm³ c) the volume of the cube in cm2
The ratio of the surface area of a cube to its volume is 2:1.Calculate: a) the length of the edge of the cube in cm b) the volume of the cube in cm³ c) the volume of the cube in cm2 - Vertical prism
 The base of the vertical prism is a rhombus with diagonals of 24 cm and 10 cm. Suppose the shell area is 52% of the total surface area of the prism. Calculate its surface.
The base of the vertical prism is a rhombus with diagonals of 24 cm and 10 cm. Suppose the shell area is 52% of the total surface area of the prism. Calculate its surface. - Divide line segment
 Find the point P on line segment AB, such that |AP| = r |AB|. Coordinates of endpoints: A = (−2, 0, 1), B = (10, 8, 5), ratio r = 1/4.
Find the point P on line segment AB, such that |AP| = r |AB|. Coordinates of endpoints: A = (−2, 0, 1), B = (10, 8, 5), ratio r = 1/4. - The sequence
 Find the nth term of the progression 2,6,12,20...
Find the nth term of the progression 2,6,12,20... - Two pots
 Two similar pots have 16 cm and 10 cm heights if the smaller pot holds 0,75 l. Find the capacity of the larger pot
Two similar pots have 16 cm and 10 cm heights if the smaller pot holds 0,75 l. Find the capacity of the larger pot - Volume and surface
 Calculate the volume and surface area of the cylinder when the cylinder height and base diameter are in a ratio of 3:4, and the area of Lateral Surface Area (LSA) is 24 dm².
Calculate the volume and surface area of the cylinder when the cylinder height and base diameter are in a ratio of 3:4, and the area of Lateral Surface Area (LSA) is 24 dm². - Tower
 Charles built a tower of cubes with an edge 2 cm long. In the lowest layer, there were six cubes (in one row) in six rows. In each subsequent layer, always one cube and one row less. What volume in cm³ did the whole tower have?
Charles built a tower of cubes with an edge 2 cm long. In the lowest layer, there were six cubes (in one row) in six rows. In each subsequent layer, always one cube and one row less. What volume in cm³ did the whole tower have? - Three-sided prism
 Find the area of the largest wall of a three-sided prism, with a height of 4 dm and an edge length of 5 cm and 6 cm.
Find the area of the largest wall of a three-sided prism, with a height of 4 dm and an edge length of 5 cm and 6 cm. - The escalator
 I run up the escalator constantly in the stairs' direction and write down the number of steps A we climbed. Then we turned around, ran it at the same constant speed in the opposite direction, and wrote down the number of steps B that I climbed. If A = 24
I run up the escalator constantly in the stairs' direction and write down the number of steps A we climbed. Then we turned around, ran it at the same constant speed in the opposite direction, and wrote down the number of steps B that I climbed. If A = 24 - Quadrilateral pyramid
 The volume of a regular quadrilateral pyramid is 72 cm³. Its height is equal to the length of the base edge. Calculate the length of the base and the surface of the pyramid.
The volume of a regular quadrilateral pyramid is 72 cm³. Its height is equal to the length of the base edge. Calculate the length of the base and the surface of the pyramid. - Decreases 5625
 How much percent will the surface and volume of the cube decrease if the diagonal decreases by 10%? b) if the diagonal increases by 10%?
How much percent will the surface and volume of the cube decrease if the diagonal decreases by 10%? b) if the diagonal increases by 10%? - Determine: 10182
 The lengths of the edges of two cubes are in the ratio 1:2, determine: a) the ratio of the area of the wall of the smaller cube to the area of the wall of the larger cube. b) the ratio of the surface of the smaller cube to the surface of the larger cube.
The lengths of the edges of two cubes are in the ratio 1:2, determine: a) the ratio of the area of the wall of the smaller cube to the area of the wall of the larger cube. b) the ratio of the surface of the smaller cube to the surface of the larger cube. - Mouse Hryzka
 Mouse Hryzka found 27 identical cubes of cheese. She first put a large cube out of them and then waited for a while before the cheese cubes stuck together. Then, she will eat the middle cube from every wall of the big cube. Then she also eats the cube in
Mouse Hryzka found 27 identical cubes of cheese. She first put a large cube out of them and then waited for a while before the cheese cubes stuck together. Then, she will eat the middle cube from every wall of the big cube. Then she also eats the cube in - Slant surface
 The surface of the rotating cone and its base area is in the ratio 18:5. Determine the volume of the cone if its body height is 12 cm.
The surface of the rotating cone and its base area is in the ratio 18:5. Determine the volume of the cone if its body height is 12 cm.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
