Circle practice problems - page 31 of 50
Number of problems found: 992
- Ruler and compass
 Use a ruler and compass to construct a triangle ABC with AB 5cm BAC 60° and ACB 45°.
Use a ruler and compass to construct a triangle ABC with AB 5cm BAC 60° and ACB 45°. - North Pole
 What is the shortest distance across the globe's surface on a scale of 1:1,000,000 from the equator to the North Pole?
What is the shortest distance across the globe's surface on a scale of 1:1,000,000 from the equator to the North Pole? - Right triangle
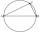 Draw a right triangle ABC if |AB| = 5 cm |BC| = 3 cm, |AC| = 4 cm. Draw Thales circle above the hypotenuse of the triangle ABC.
Draw a right triangle ABC if |AB| = 5 cm |BC| = 3 cm, |AC| = 4 cm. Draw Thales circle above the hypotenuse of the triangle ABC. - Circumscribing
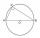 Find the radius of the circumscribed circle to the right triangle with legs 6 cm and 3 cm.
Find the radius of the circumscribed circle to the right triangle with legs 6 cm and 3 cm. - Construct
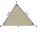 Construct a triangle ABC inscribed circle with a radius r = 2 cm and an angle alpha = 50 degrees = 8 cm. Make a sketch, analysis, construction, and description.
Construct a triangle ABC inscribed circle with a radius r = 2 cm and an angle alpha = 50 degrees = 8 cm. Make a sketch, analysis, construction, and description. - Perpendiculars 64574
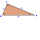 Calculate the circle radius circumscribed by a right triangle whose perpendiculars are 10 cm and 24 cm long.
Calculate the circle radius circumscribed by a right triangle whose perpendiculars are 10 cm and 24 cm long. - Circular 36163
 The circular park has an area of 31400 m². A trail runs across the center of the park. How long is it?
The circular park has an area of 31400 m². A trail runs across the center of the park. How long is it? - Square circles
 Calculate the length of the described and inscribed circle to the square ABCD with a side of 5cm.
Calculate the length of the described and inscribed circle to the square ABCD with a side of 5cm. - Coat of arms
 The class created its coat of arms, which had a shape composed of an isosceles trapezoid ABCD (shorter base is a = 4.5 cm long, longer 2a = 9 cm, trapezoid height 6 cm) and a semicircle with center S and diameter AB. Three identical isosceles triangles fo
The class created its coat of arms, which had a shape composed of an isosceles trapezoid ABCD (shorter base is a = 4.5 cm long, longer 2a = 9 cm, trapezoid height 6 cm) and a semicircle with center S and diameter AB. Three identical isosceles triangles fo - OK circle
 The right triangle has hypotenuse long 33 and one cathetus long 17. Calculate the radius (circumradius) of the circle described.
The right triangle has hypotenuse long 33 and one cathetus long 17. Calculate the radius (circumradius) of the circle described. - Suppose
 Suppose you know that the length of a line segment is 15, x2=6, y2=14, and x1= -3. Find the possible value of y1. Is there more than one possible answer? Why or why not?
Suppose you know that the length of a line segment is 15, x2=6, y2=14, and x1= -3. Find the possible value of y1. Is there more than one possible answer? Why or why not? - Pipe cross section
 The pipe has an outside diameter of 1100 mm, and the pipe wall is 100 mm thick. Calculate the cross-section of this pipe.
The pipe has an outside diameter of 1100 mm, and the pipe wall is 100 mm thick. Calculate the cross-section of this pipe. - Annulus
 Two concentric circles form an annulus with a width of 10 cm. The radius of the smaller circle is 20 cm. Calculate the area of the annulus.
Two concentric circles form an annulus with a width of 10 cm. The radius of the smaller circle is 20 cm. Calculate the area of the annulus. - Pipeline
 How much percent has the pipe cross-section area changed (reduced) if the circular shape is changed to square with the same perimeter?
How much percent has the pipe cross-section area changed (reduced) if the circular shape is changed to square with the same perimeter? - Square and circles
 Square with sides 68 km is circumscribed and inscribed with circles. Determine the radiuses of both circles.
Square with sides 68 km is circumscribed and inscribed with circles. Determine the radiuses of both circles. - Clocks
 What distance will describe the tip of a minute hand 6 cm long for 20 minutes when we know the starting position with finally enclosed hands at each other at 120°?
What distance will describe the tip of a minute hand 6 cm long for 20 minutes when we know the starting position with finally enclosed hands at each other at 120°? - Goat
 The meadow is a circle with a radius r = 20 m. How long must a rope tie a goat to the pin on the meadow's perimeter to allow the goat to eat half of the meadow?
The meadow is a circle with a radius r = 20 m. How long must a rope tie a goat to the pin on the meadow's perimeter to allow the goat to eat half of the meadow? - Dimensions 82414
 The flag of Brazil has a yellow diamond on a green field with a blue circle inside. If we had a flag with dimensions of 70 cm x 50 cm, the rhombus would have a side 35 cm long and a height of 30 cm. Indicate with fractions in basic form what part of the f
The flag of Brazil has a yellow diamond on a green field with a blue circle inside. If we had a flag with dimensions of 70 cm x 50 cm, the rhombus would have a side 35 cm long and a height of 30 cm. Indicate with fractions in basic form what part of the f - Calculate 71744
 The triangle that connects on the dial: a) 2,7,9 b) 3,6,10 Calculate the size of the interior angles.
The triangle that connects on the dial: a) 2,7,9 b) 3,6,10 Calculate the size of the interior angles. - Circle from string
 Martin has a long 628 mm string. He makes a circle from it. Calculate the radius of the circle.
Martin has a long 628 mm string. He makes a circle from it. Calculate the radius of the circle.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
