Circle practice problems - page 32 of 50
Number of problems found: 992
- The big clock
 The big clock hands stopped at a random moment. What is the probability that: a) a small hand showed the time between 1:00 and 3:00. b) the big hand was in the same area as a small hand in the role of a)? c) did the hours just show the time between 21:00
The big clock hands stopped at a random moment. What is the probability that: a) a small hand showed the time between 1:00 and 3:00. b) the big hand was in the same area as a small hand in the role of a)? c) did the hours just show the time between 21:00 - Points on circle
 The Cartesian coordinate system with the origin O is a sketched circle k /center O; radius r=2 cm/. Write all the points that lie on a circle k and whose coordinates are integers. Write all the points on the circle I with center O and radius r=5 cm, whose
The Cartesian coordinate system with the origin O is a sketched circle k /center O; radius r=2 cm/. Write all the points that lie on a circle k and whose coordinates are integers. Write all the points on the circle I with center O and radius r=5 cm, whose - Ratio of sides
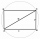 Calculate the area of a circle with the same circumference as the circumference of the rectangle inscribed with a circle with a radius of r 9 cm so that its sides are in a ratio of 2 to 7.
Calculate the area of a circle with the same circumference as the circumference of the rectangle inscribed with a circle with a radius of r 9 cm so that its sides are in a ratio of 2 to 7. - Construction: 81894
 Construct a rhombus that has a side length of 5 cm and a height of 4.5 cm. Outline: Analysis: Construction: Method:
Construct a rhombus that has a side length of 5 cm and a height of 4.5 cm. Outline: Analysis: Construction: Method: - Determine 54881
 On the tourist map with a scale of 1:50000, the section of the railway line between Bobrová Lhota and Javořiště is replaced by an arc of a circle with a radius of 6 cm. The arc is 90°. Determine the actual length of the track between the two villages.
On the tourist map with a scale of 1:50000, the section of the railway line between Bobrová Lhota and Javořiště is replaced by an arc of a circle with a radius of 6 cm. The arc is 90°. Determine the actual length of the track between the two villages. - Equation of a circle
 Write the general equation of a circle with center S(2;5) and point B(5;6) lying on this circle.
Write the general equation of a circle with center S(2;5) and point B(5;6) lying on this circle. - Mrak - cloud
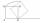 It is given segment AB, which is 12 cm in length, on which one side of the square MRAK is laid. MRAK's side length is 2 cm shown. MRAK gradually flips along the line segment AB, and point R leaves a paper trail. Draw the whole track of point R until the s
It is given segment AB, which is 12 cm in length, on which one side of the square MRAK is laid. MRAK's side length is 2 cm shown. MRAK gradually flips along the line segment AB, and point R leaves a paper trail. Draw the whole track of point R until the s - Inscribed rectangle
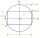 What is the perimeter of a rectangle inscribed in a circle whose diameter is 5 dm long? Answer: 14 dm
What is the perimeter of a rectangle inscribed in a circle whose diameter is 5 dm long? Answer: 14 dm - V-belt
 Calculate the length of the belt on pulleys with diameters of 105 mm and 393 mm at shaft distance 697 mm.
Calculate the length of the belt on pulleys with diameters of 105 mm and 393 mm at shaft distance 697 mm. - Isosceles IV
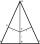 In an isosceles triangle ABC is |AC| = |BC| = 13 and |AB| = 10. Calculate the radius of the inscribed (r) and described (R) circle.
In an isosceles triangle ABC is |AC| = |BC| = 13 and |AB| = 10. Calculate the radius of the inscribed (r) and described (R) circle. - Posters
 A column with posters in the form of a cylinder is 2 m high, and its diameter is 1.7 m. What is the area in which it is possible to stick posters?
A column with posters in the form of a cylinder is 2 m high, and its diameter is 1.7 m. What is the area in which it is possible to stick posters? - Hot air balloon
 The center of the balloon is at an altitude of 600 m above the ground (AGL). The observer on earth sees the center of the balloon at an elevation angle of 38°20'. The balloon is seen from the perspective of an angle of 1°16'. Calculate the diameter of the
The center of the balloon is at an altitude of 600 m above the ground (AGL). The observer on earth sees the center of the balloon at an elevation angle of 38°20'. The balloon is seen from the perspective of an angle of 1°16'. Calculate the diameter of the - Annulus
 Calculate the area of two circles annulus k1 (S, 3 cm) and k2 (S, 5 cm).
Calculate the area of two circles annulus k1 (S, 3 cm) and k2 (S, 5 cm). - EQL triangle
 Calculate the inradius and circumradius of an equilateral triangle with side a=67 cm.
Calculate the inradius and circumradius of an equilateral triangle with side a=67 cm. - Percentage 23631
 In the shape of a rectangle, the city park, measuring 125 x 12 m, has a circular fountain with a diameter of 10 m. What percentage of this fountain represents the total area of the park?
In the shape of a rectangle, the city park, measuring 125 x 12 m, has a circular fountain with a diameter of 10 m. What percentage of this fountain represents the total area of the park? - Commemorative coins
 On the 200th anniversary of the birth of Ľudovít Štúr, the National Bank of Slovakia issued a commemorative two-euro coin in 2015, the diameter of which is 25.75 mm. The nickel-brass center is approximately 18 millimeters in diameter; the rest of the coin
On the 200th anniversary of the birth of Ľudovít Štúr, the National Bank of Slovakia issued a commemorative two-euro coin in 2015, the diameter of which is 25.75 mm. The nickel-brass center is approximately 18 millimeters in diameter; the rest of the coin - Trigonometric formula
 Determine the value of the function tg x (tangent) when cotan x = -0.8 (cotg or cotangent); x holds in the second quadrant)
Determine the value of the function tg x (tangent) when cotan x = -0.8 (cotg or cotangent); x holds in the second quadrant) - Inscribed circle
 XYZ is a right triangle with a right angle at the vertex X and an inscribed circle with a radius of 5 cm. Find the area of the triangle XYZ if XZ = 14 cm.
XYZ is a right triangle with a right angle at the vertex X and an inscribed circle with a radius of 5 cm. Find the area of the triangle XYZ if XZ = 14 cm. - Deformation 6260
 The carpet is wound on a cardboard roll in the shape of a cylinder with a diameter of d=12cm and a length of l=2m. The rolled-up carpet has an outer diameter of D=38cm, and the thickness of the rug is 8mm. What area can the carpet cover after unfolding? D
The carpet is wound on a cardboard roll in the shape of a cylinder with a diameter of d=12cm and a length of l=2m. The rolled-up carpet has an outer diameter of D=38cm, and the thickness of the rug is 8mm. What area can the carpet cover after unfolding? D - Katy 7
 Katy ordered a cylinder-shaped cake with a volume of 15.7 l. It consists of two layers. The volume of the upper layer is 4 times smaller than the volume of the lower layer. The height of both layers is the same and is equal to the radius of the upper laye
Katy ordered a cylinder-shaped cake with a volume of 15.7 l. It consists of two layers. The volume of the upper layer is 4 times smaller than the volume of the lower layer. The height of both layers is the same and is equal to the radius of the upper laye
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
