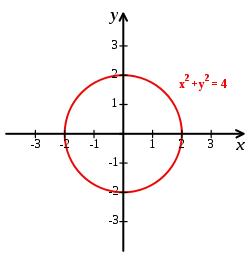
Points on circle
The Cartesian coordinate system with the origin O is a sketched circle k /center O; radius r=2 cm/. Write all the points that lie on a circle k and whose coordinates are integers. Write all the points on the circle I with center O and radius r=5 cm, whose coordinates are integers. How many points is it?
Correct answer:
Tips for related online calculators
Do you solve Diofant problems and are looking for a calculator of Diofant integer equations?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
geometryalgebraarithmeticplanimetricsnumbersGrade of the word problem
Related math problems and questions:
- Unit circle
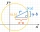In the Cartesian coordinate system, a unit circle is given on which points A and B lie. Point O is the origin and has coordinates (0,0) and point B has coordinates (1,0). The size of angle BOA is 151°. Determine the x-coordinate of point A. - X-coordinate 81737
In triangle ABC, determine the coordinates of point B if you know that points A and B lie on the line 3x-y-5=0, points A and C lie on line 2x+3y+4=0, point C lies on the x-coordinate axis, and the angle at vertex C is right. - A Cartesian framework
1. In a Cartesian framework, the functions f and g we know that: The function (f) is defined by f (x) = 2x², the function (g) is defined by g (x) = x + 3, the point (O) is the origin of the reference, and point (C) is the point of intersection of the grap - Rectangular 3478
A segment AB is drawn in the rectangular coordinate system with endpoints A [1;6] and B [5;2]. The center symmetry is the origin of the coordinate system. Find the coordinates of the center of this segment in this symmetry projection.
- Circle
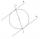The circle touches two parallel lines, p, and q, and its center lies on line a, which is the secant of lines p and q. Write the equation of the circle and determine the coordinates of the center and radius. p: x-10 = 0 q: -x-19 = 0 a: 9x-4y+5 = 0 - Direction vector
The line p is given by the point P [- 0,5; 1] and the direction vector s = (1,5; - 3) determines: A) value of parameter t for points X [- 1,5; 3], Y [1; - 2] lines p B) whether the points R [0,5; - 1], S [1,5; 3] lie on the line p C) parametric equations - Chord
It is given to a circle k(r=6 cm), and the points A and B such that |AB| = 8 cm lie on k. Calculate the distance of the center of circle S to the midpoint C of segment AB.
