Isolating a variable in the formula - math word problems - page 19 of 45
Number of problems found: 888
- Sphere in cone
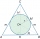A sphere is inscribed in the cone (the intersection of their boundaries consists of a circle and one point). The ratio of the ball's surface and the area of the base is 4:3. A plane passing through the axis of a cone cuts the cone in an isosceles triangle - Distance of points
A regular quadrilateral pyramid ABCDV is given, in which edge AB = a = 4 cm and height v = 8 cm. Let S be the center of the CV. Find the distance of points A and S. - Quadrilateral pyramid
The height of a regular quadrilateral pyramid is 6.5 cm, and the angle between the base and the side wall is 42°. Calculate the surface area and volume of the body—round calculations to 1 decimal place. - Diagonal BD
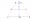Find the length of the diagonal BD in a rectangular trapezoid ABCD with a right angle at vertex A when/AD / = 8,1 cm and the angle DBA is 42°
- Equation of the circle
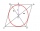Find the equation of the circle inscribed in the rhombus ABCD where A[1, -2], B[8, -3], and C[9, 4]. - Ratio of squares
A circle is given, and a square is inscribed. The smaller square is inscribed in a circular arc formed by the square's side and the circle's arc. What is the ratio of the areas of the large and small squares? - Triangular prism
The triangular prism has a base in the shape of a right triangle, the legs of which are 9 cm and 40 cm long. The height of the prism is 20 cm. What is its volume cm³? And the surface cm²? - Roots and coefficient
In the equation 2x² + bx-9 = 0 is one root x1 = -3/2. Determine the second root and the coefficient b. - Equilateral cone
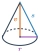We pour so much water into a container with the shape of an equilateral cone, the base of which has a radius r = 6 cm, that one-third of the volume of the cone is filled. How high will the water reach if we turn the cone upside down?
- Coins
The money - -coins are minted from the hardest bronze, which contains copper and tin in a ratio of 41:9. How much copper and tin are in 2kg of bronze money? - Sailboat
The 20 m long sailboat has an 8 m high mast in the middle of the deck. The top of the mast is fixed to the bow and stern with a steel cable. Determine how much cable is needed to secure the mast and what angle the cable will make with the ship's deck. - Square and circles The square in the picture has a side length of a = 20 cm. Circular arcs have centers at the vertices of the square. Calculate the areas of the colored unit. Express area using side a.
- Planting 27201
In the forest, there are 84 workers employed in planting saplings. Working 10 hours a day, they would finish the job in 24 days. After 7 days, 14 workers leave. How long will it take the others to finish planting the saplings if they work 12 hours a day f - Meneal's 26771
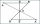Show (using Meneal's theorem) that the center of gravity divides the line in a 1:2 ratio.
- Pentadecagon
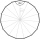Calculate the area of a regular 15-side polygon inscribed in a circle with a radius r = 4. Express the result to two decimal places. - The rectangle
In the rectangle ABCD, the distance of its center from line AB is 3 cm greater than from line BC. The circumference of the rectangle is 52 cm. Calculate the area of the rectangle. Express the result in cm². - Dodecagon
Calculate the size of the smaller angles determined by lines A1 A4 and A2 A10 in the regular dodecagon A1A2A3. .. A12. Express the result in degrees. - Circumference 26651
A rectangle with sides of lengths a, b (cm) has a circumference of 100 cm. The dependence of its area P (in cm2) on the number a can be expressed by the quadratic function P = sa + ta². Find the coefficients s, t. - Rectangular 26641
The area of the work surface of the rectangular table is 70 dm2, and its perimeter is 34 dm. Determine (in dm) the length of the shorter side of this table.
An observer standing west of the tower sees its top at an altitude angle of 45 degrees. After moving 50 meters to the south, he sees its top at an altitude angle of 30 degrees. How tall is the tower?Do you have unsolved problem that you need help? Ask a question, and we will try to solve it. Solving math problems.
