Geometry - math word problems - page 132 of 162
Number of problems found: 3238
- Measuring 6188
 Find the length of the cube's edge and its volume is equal to 60% of the volume of a block measuring 7 cm, 8 cm, and 6 cm.
Find the length of the cube's edge and its volume is equal to 60% of the volume of a block measuring 7 cm, 8 cm, and 6 cm. - Determine 2429
 Determine the length of the cube's edge, the volume of which is equal to 60% of the volume of a block measuring 7cm, 8cm, and 6cm.
Determine the length of the cube's edge, the volume of which is equal to 60% of the volume of a block measuring 7cm, 8cm, and 6cm. - Midpoint of segment
 Find the distance and midpoint between A(1,2) and B(5,5).
Find the distance and midpoint between A(1,2) and B(5,5). - Perpendicular 82488
 For the volumes of a perpendicular prism and a pyramid with the same base and height: A) the volumes are equal B) the volume of a pyramid is three times smaller than the volume of a prism C) the ratio of the volumes of the prism and the pyramid is 1:3 D)
For the volumes of a perpendicular prism and a pyramid with the same base and height: A) the volumes are equal B) the volume of a pyramid is three times smaller than the volume of a prism C) the ratio of the volumes of the prism and the pyramid is 1:3 D) - Construct 1
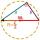 Construct a triangle ABC, a = 7 cm, b = 9 cm with a right angle at C, and construct the axis of all three sides. Measure the length of side c (and write).
Construct a triangle ABC, a = 7 cm, b = 9 cm with a right angle at C, and construct the axis of all three sides. Measure the length of side c (and write). - Circumference 30781
 How many square decimeters of decorative paper are needed to make cone-shaped carnival hats for 46 first-graders if the first-graders head circumference is 49 cm and the cap height is 33 cm? Is it necessary to add 3% paper to the folds?
How many square decimeters of decorative paper are needed to make cone-shaped carnival hats for 46 first-graders if the first-graders head circumference is 49 cm and the cap height is 33 cm? Is it necessary to add 3% paper to the folds? - Volume of three cuboids
 Calculate the total volume of all cuboids for which the edges' sizes are in a ratio of 1:2:3, and one of the edges has a size of 6 cm.
Calculate the total volume of all cuboids for which the edges' sizes are in a ratio of 1:2:3, and one of the edges has a size of 6 cm. - Lathe
 Calculate the percentage of waste if the cube with 44 cm long edge is lathed to the cylinder with a maximum volume.
Calculate the percentage of waste if the cube with 44 cm long edge is lathed to the cylinder with a maximum volume. - Lathe
 From the cube of edge, 41 cm was a lathed maximum cylinder. What percentage of the cube is left as waste after being lathed?
From the cube of edge, 41 cm was a lathed maximum cylinder. What percentage of the cube is left as waste after being lathed? - Hectoliters - tank
 A cylindrical tank with a base diameter of 1.2 m is supposed to hold 17 hectoliters of water. How many square meters of sheet metal are needed to make it? We calculate if 2% of the surfaces are for joints and waste.
A cylindrical tank with a base diameter of 1.2 m is supposed to hold 17 hectoliters of water. How many square meters of sheet metal are needed to make it? We calculate if 2% of the surfaces are for joints and waste. - Sheet metal troughs
 A farmer orders sheet metal troughs from a tinsmith for loading calves on pasture. The tinsmith looks at a picture of the trough and estimates how much sheet metal he will need for one trough. Determine the sheet metal consumption, add 15% for waste and j
A farmer orders sheet metal troughs from a tinsmith for loading calves on pasture. The tinsmith looks at a picture of the trough and estimates how much sheet metal he will need for one trough. Determine the sheet metal consumption, add 15% for waste and j - Concrete column
 The concrete column of the highway bridge has the shape of a block with dimensions of 1m x 0.8m x 25m. Crane should lift it to a height of 20m. What is the power of his engine if the lifting takes 2 minutes?
The concrete column of the highway bridge has the shape of a block with dimensions of 1m x 0.8m x 25m. Crane should lift it to a height of 20m. What is the power of his engine if the lifting takes 2 minutes? - Considering 67324
 Susan has an old stool - a cube with an edge length of 80 cm. She wants to sew a new cover for her. How many square meters does the fabric consume, considering adding 15% for stitching and folds?
Susan has an old stool - a cube with an edge length of 80 cm. She wants to sew a new cover for her. How many square meters does the fabric consume, considering adding 15% for stitching and folds? - Right triangle
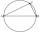 Draw a right triangle ABC if |AB| = 5 cm |BC| = 3 cm, |AC| = 4 cm. Draw Thales circle above the hypotenuse of the triangle ABC.
Draw a right triangle ABC if |AB| = 5 cm |BC| = 3 cm, |AC| = 4 cm. Draw Thales circle above the hypotenuse of the triangle ABC. - Cuboid and ratio
 A cuboid has a volume of 810 cm³. The lengths of edges from the same vertex are in a ratio of 2:3:5. Find the dimensions of a cuboid.
A cuboid has a volume of 810 cm³. The lengths of edges from the same vertex are in a ratio of 2:3:5. Find the dimensions of a cuboid. - Intersections 2557
 How many intersections do circles with radii of 10 cm and 6 cm have if the distance between their centers is 3 cm?
How many intersections do circles with radii of 10 cm and 6 cm have if the distance between their centers is 3 cm? - Dimensions 7932
 The volume of the block is 5760 cm³. For the dimensions of a given block, a: b = 4:3, b: c = 2:5 Calculate its surface.
The volume of the block is 5760 cm³. For the dimensions of a given block, a: b = 4:3, b: c = 2:5 Calculate its surface. - Calculate 82409
 The lamp shade should be formed by the shell of a cone with a base diameter of 48 cm and a side of 32 cm. Calculate how much material will be needed to make it, assuming 8% waste
The lamp shade should be formed by the shell of a cone with a base diameter of 48 cm and a side of 32 cm. Calculate how much material will be needed to make it, assuming 8% waste - How many 9
 How much percent volume remains of a sphere if the diameter decrease 3×?
How much percent volume remains of a sphere if the diameter decrease 3×? - Volume ratio
 Calculate the volume ratio of balls circumscribed (diameter r) and inscribed (diameter ϱ) into an equilateral rotating cone.
Calculate the volume ratio of balls circumscribed (diameter r) and inscribed (diameter ϱ) into an equilateral rotating cone.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
