Grade - math word problems - page 883 of 949
Number of problems found: 18978
- Number
 Determine an unknown number if you know that the difference between five times and triple of number is 54.
Determine an unknown number if you know that the difference between five times and triple of number is 54. - Obtuse angle
 Line OH is the height of the triangle DOM, and line MN is the bisector of angle DMO. the Obtuse angle between the lines MN and OH is four times larger than the angle DMN. What size is the angle DMO? (see attached image)
Line OH is the height of the triangle DOM, and line MN is the bisector of angle DMO. the Obtuse angle between the lines MN and OH is four times larger than the angle DMN. What size is the angle DMO? (see attached image) - Parcel
 Both dimensions of the rectangular parcel were increased by 31%. By how much % has it increased its acreage?
Both dimensions of the rectangular parcel were increased by 31%. By how much % has it increased its acreage? - Simply equation
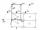 Solve this equation for x: 9x-6(x-1)=5(x+2)-14
Solve this equation for x: 9x-6(x-1)=5(x+2)-14 - Sphere in cone
 A sphere of radius 3 cm describes a cone with minimum volume. Determine cone dimensions.
A sphere of radius 3 cm describes a cone with minimum volume. Determine cone dimensions. - Unknown integer
 Find the smallest integer: Divided by 2, the remainder is 1. divided by 3. The remainder is 2. divided by 4. The remainder is 3. Divided by eight, the remainder is 7. Divided by 9, the remainder is 8.
Find the smallest integer: Divided by 2, the remainder is 1. divided by 3. The remainder is 2. divided by 4. The remainder is 3. Divided by eight, the remainder is 7. Divided by 9, the remainder is 8. - Parallelogram ABCD
 The area of parallelogram ABCD is 906 cm². Points M and N are the midpoints of the sides AB and BC. What is the area of a quadrilateral MBND?
The area of parallelogram ABCD is 906 cm². Points M and N are the midpoints of the sides AB and BC. What is the area of a quadrilateral MBND? - Hexadecimal number
 What will the hexadecimal number 293 be as a decimal number?
What will the hexadecimal number 293 be as a decimal number? - Bonbons 2
 Kilo sweets will cost 260 CZK. The first type has a price per 320 kg, and the second type is 240 CZK per kg. How many kilos of both kinds of sweets need to prepare a 81 kg mixture?
Kilo sweets will cost 260 CZK. The first type has a price per 320 kg, and the second type is 240 CZK per kg. How many kilos of both kinds of sweets need to prepare a 81 kg mixture? - Circles
 The area of a circle inscribed in a square is 7. What is the area of a circle circumscribed around a square?
The area of a circle inscribed in a square is 7. What is the area of a circle circumscribed around a square? - Cone
 Into rotating cone with dimensions r = 8 cm and h = 8 cm is an inscribed cylinder with maximum volume so that the cylinder axis is perpendicular to the cone's axis. Determine the dimensions of the cylinder.
Into rotating cone with dimensions r = 8 cm and h = 8 cm is an inscribed cylinder with maximum volume so that the cylinder axis is perpendicular to the cone's axis. Determine the dimensions of the cylinder. - Freight train
 The train carries 525 tons of limestone in 29 wagons. Wagons are 15 tonne and 20 tons. How many are 15 ton, and how many are 20 ton wagons?
The train carries 525 tons of limestone in 29 wagons. Wagons are 15 tonne and 20 tons. How many are 15 ton, and how many are 20 ton wagons? - Football season
 Throughout the football season gave, Adam 23 goals more than Brano and 16 goals less than Karol. Edo gave the six goals more Dušan. Karol gave five more than Edo. Brano and Edo gave together 17 goals. How many goals did you give each boy, and how many goa
Throughout the football season gave, Adam 23 goals more than Brano and 16 goals less than Karol. Edo gave the six goals more Dušan. Karol gave five more than Edo. Brano and Edo gave together 17 goals. How many goals did you give each boy, and how many goa - Cuboid
 Cuboid ABCDEFGH with 10 cm height has a base edge length 6 cm and 8 cm. Determine the angle between the body diagonal and the base plane (round to degrees).
Cuboid ABCDEFGH with 10 cm height has a base edge length 6 cm and 8 cm. Determine the angle between the body diagonal and the base plane (round to degrees). - Chicken and rabbits (classic)
 Grandmother bred chickens and rabbits. It found that the yard has 25 heads and 70 legs. How many chickens and rabbits breed in the yard?
Grandmother bred chickens and rabbits. It found that the yard has 25 heads and 70 legs. How many chickens and rabbits breed in the yard? - Meat
 Half a kilogram of pork and three-quarters of a kilogram of beef cost a total 6.2 Euro. One-quarter of a kilogram of beef and 1 kilogram of pork costs 5.9 Euro. Find the price of 1 kg of each type of meat.
Half a kilogram of pork and three-quarters of a kilogram of beef cost a total 6.2 Euro. One-quarter of a kilogram of beef and 1 kilogram of pork costs 5.9 Euro. Find the price of 1 kg of each type of meat. - Product - quadratic equation
 The product of the two numbers is 900. If we increase the lowest number by two, its product will increase by 150. Determine both numbers.
The product of the two numbers is 900. If we increase the lowest number by two, its product will increase by 150. Determine both numbers. - Ratio of perimeters
 Rectangle ABCD has dimensions 11 cm and 7 cm, and KLMN rectangle has dimensions 10 cm and 10 cm. Calculate the ratio of the perimeter ABCD and perimeter KLMN.
Rectangle ABCD has dimensions 11 cm and 7 cm, and KLMN rectangle has dimensions 10 cm and 10 cm. Calculate the ratio of the perimeter ABCD and perimeter KLMN. - Cylinder - h2
 The cylinder volume is 3 liters. The base area is 1.1 dm². Calculate the height of the cylinder.
The cylinder volume is 3 liters. The base area is 1.1 dm². Calculate the height of the cylinder. - The carpet
 How many meters of carpet 90 cm wide need to cover the floor room, which has a rectangular shape with lengths of 4.8 m and 2.4 m, if the number of pieces on the carpet is needed to be lowest?
How many meters of carpet 90 cm wide need to cover the floor room, which has a rectangular shape with lengths of 4.8 m and 2.4 m, if the number of pieces on the carpet is needed to be lowest?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
